首先是理解透彻最常接触到的这 6 个三角函数, 牢牢记住掌握相应的公式。

在三角函数中, 通常用希腊字母 θ 表示角, 单位圆(半径为 1,且圆心是原点)上一点到 x 轴的距离是这个角的正弦 sine , 到 y 轴的距离则是这个角的余弦 cosine. 观察下图很好地解释了正弦和余弦是怎么回事。

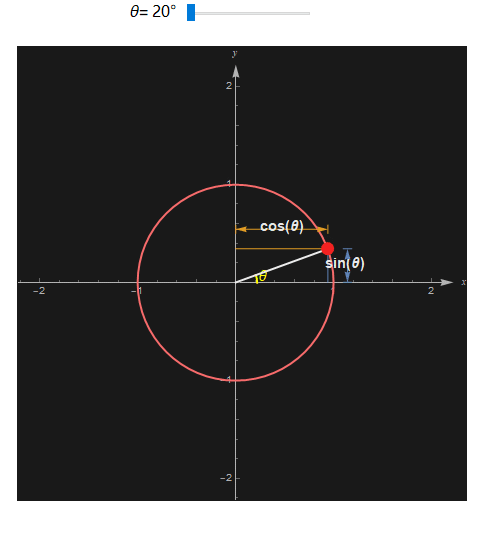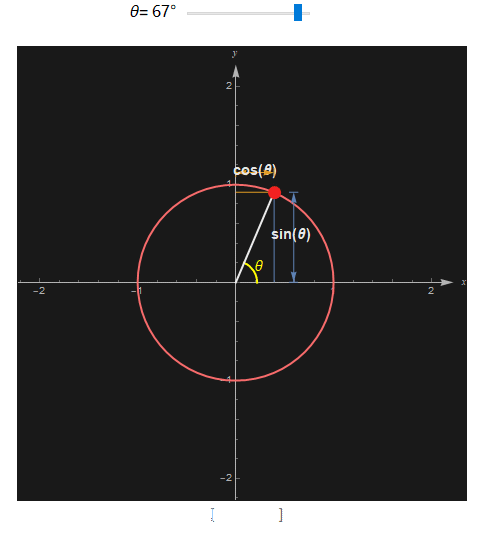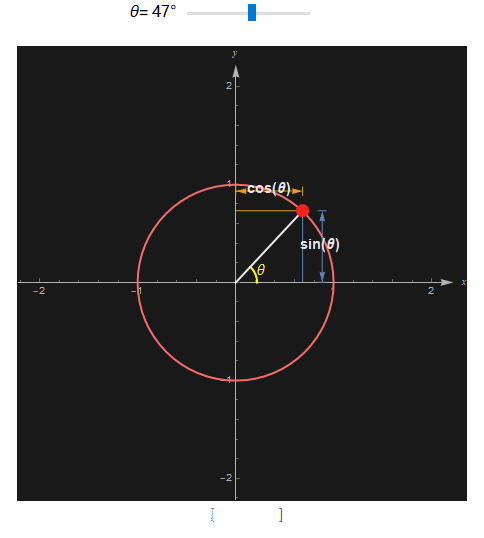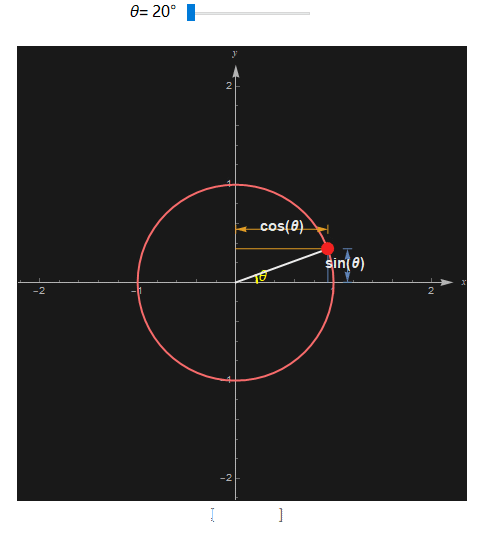
一个角的正切 tangent(tan) 是 sin 除以cos, 余切 cotangent (cot)则是 cos 除以 sin。

对 tan 和 cot 有一种漂亮的几何解释, 如果过 θ 角单位圆上的点, 画出圆的切线, 那么切线和 x 轴交点之间的距离, 就是这个角度的 tan , 这个点与切线和 y 轴的交点的距离, 就是这个角度的 cot。这种解释能让人直观感受这两个值的意义. 观察下面动图, 看看余切何时变小, 正切何时变大。

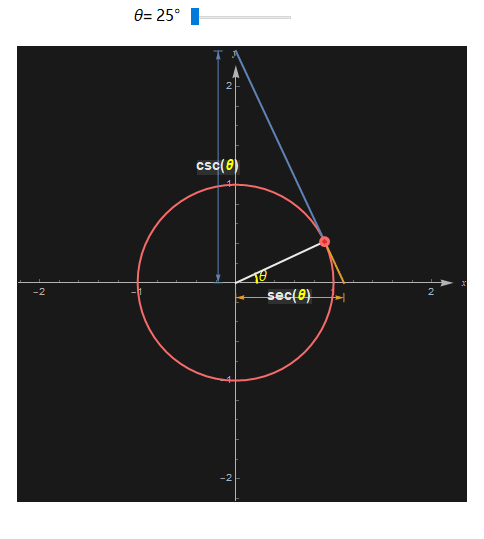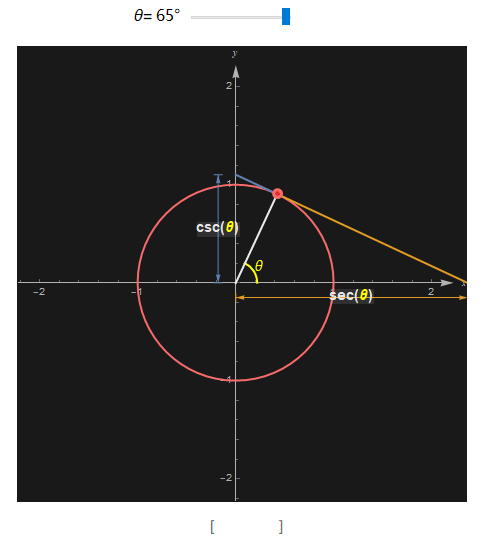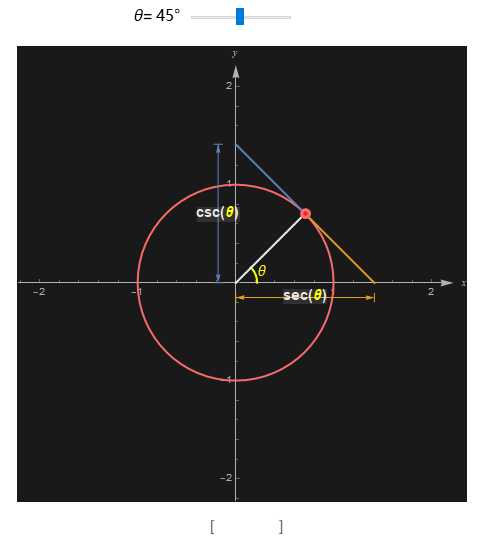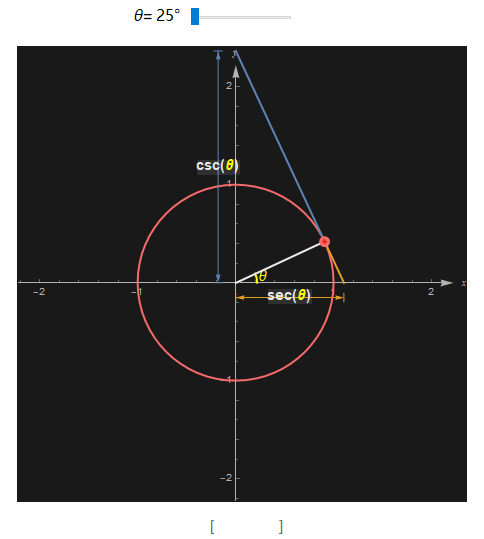
类似地, 正割secant(sec) 的定义是 1/cos, 而余割cosecant (csc)的定义是 1/sin. 在可以根据下图所示的两个相似三角形来证明(感兴趣的可以动手做下)。

并且 sec 和 csc 也有类似的几何解释, 当切线与 x 轴的交点到原点的距离就是这个角度的 sec , 而切线与 y 轴的交点到原点的距离则是这个角度的 csc。

还有一点值得注意的地方, sine, tan 和 sect 对应线段的长度都与 x 轴有关系。

而 cos, cot和 csc 对应的线段长度都与 y 轴有关系, 我们将这6个三角函数它们一并绘制出来。

三角函数之间有互余(complementary)的关系, 就是说两个角的和为 π/2。

我想这里再用 3 张图来表示下互余的关系:

上面就是制作的图解三角函数例子, 希望对你及各位学子在征服三角函数的过程中有一点帮助。部分内容取自网络。