1993年，克林顿政府决定终止已经耗资30亿美元的超导超级对撞机项目。正在洛斯阿拉莫斯国家实验室负责高能物理项目的杰弗里·韦斯特，只好决定把自己的兴趣转向生物学领域。他说：“我当时的本能反应是：生物学几乎肯定会成为21世纪占据主导地位的学科，但它若要真正成功，就必须接受物理学赖以取得成功的定量、分析和预测这样的文化……一个基于数学或可计算的基本原理而构建的理论框架”。《规模》这本书，就是一次这样的尝试。

在韦斯特之前，已经有物理学家在生物学界取得了极大的成功。比如弗朗西斯·克里克和詹姆斯·沃森运用晶体Ｘ射线衍射的方法揭示了ＤＮＡ的双螺旋结构；比如薛定谔撰写的科普著作《生命是什么》，主张物理和化学的基本原理同样可以用来阐释生命的现象和本质，由此奠定了分子生物学的基础。而韦斯特则聚焦于与规模相关的生物学问题：

为什么哥斯拉那么大的怪兽不可能存在？

我和我儿子都发烧了，而我儿子的体重是我的一半，如果我吃两片退烧药合适的话，我儿子应该吃多少？

为什么哺乳动物小到仓鼠，大到蓝鲸，一生的心跳都是15亿次？

古希腊诗人阿基罗库斯说“狐狸知道很多小事，而刺猬知道一件大事。”在物理学家看来，生物学家们汲汲于表面现象，是知道很多小事的狐狸。而物理学家却有能力透过表面看到本质，他们是那只知道一件大事的刺猬。这件大事是什么呢？就是自然界、生物界千奇百怪的表象背后，有通行的简单规则。并且，这个规则可以用数学公式表达出来。

比如，为什么不会有哥斯拉那么大的怪兽。这问题在物理学家眼里好简单：如果我们身体的各个尺寸增加一倍，那么，我们的重量就会增加到八倍，即23；但是，骨骼支撑体重能力的增加，却是与骨头的截面积成正比的，也就是说，只增加到四倍，即22。所以，人也好，树也好，哥斯拉也好，都无法无限制地生长。“否则”，伽里略说，“就会被自身的重量压垮”。工程师们都知道，如果造一座大一倍的桥，桥墩的半径也只增加一倍可不够。桥墩的半径大概得是以前的2.84倍，即根号8。

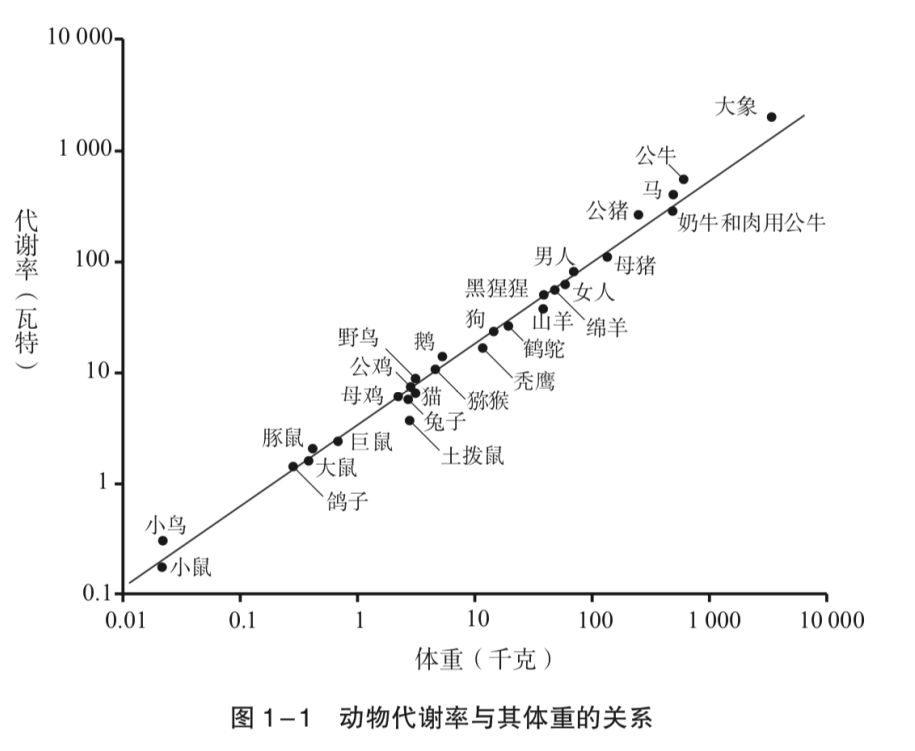
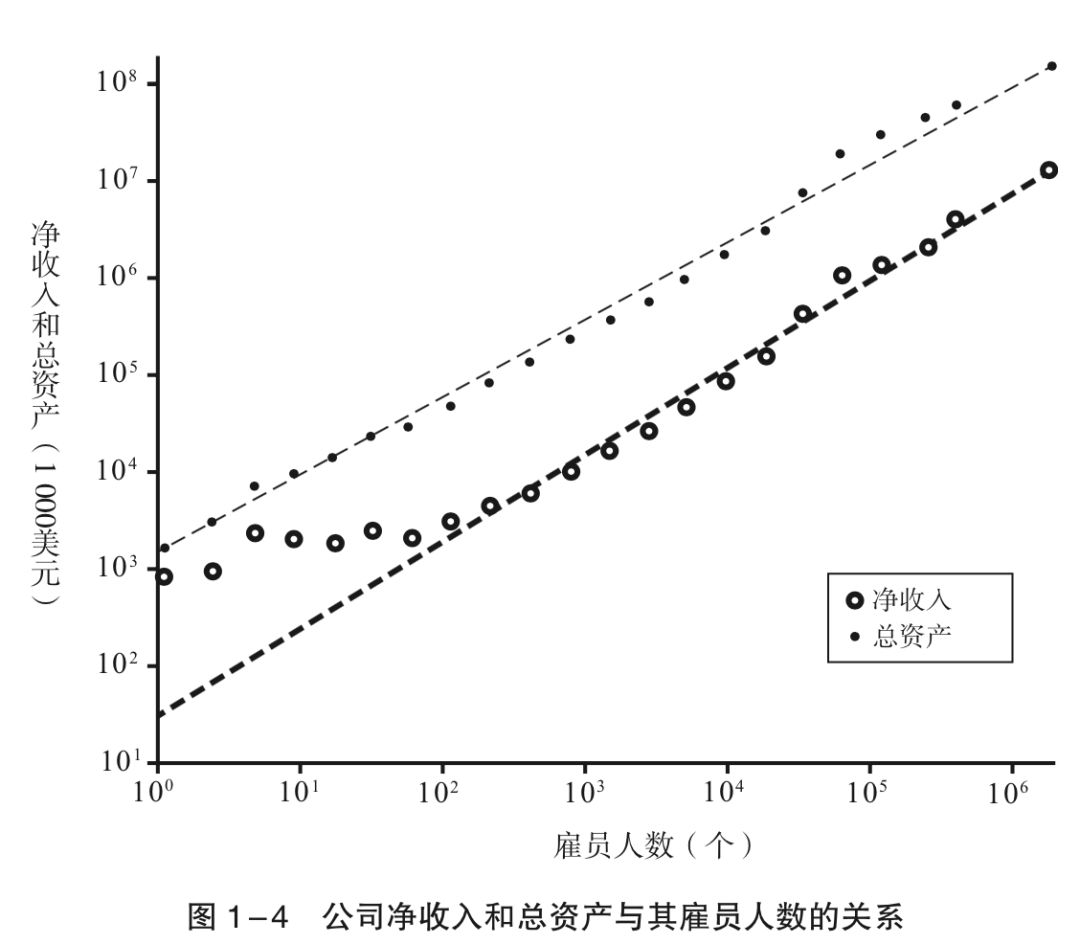
类似这种简单的“边长增加一倍、面积就增加到四倍、体积就增加到八倍”的幂函数，在形状怪异的、黏糊糊的生物界，存在吗？答案是肯定的。1932年，瑞士生物学家克莱伯就发表了论文：各种动物的基础代谢率，与体重的3/4次幂成正比。这个“3/4次幂”是什么意思？韦斯特在书中举的例子是：大象体重是老鼠的一万倍（104），那么，大象的代谢率只是老鼠的1000倍（103）。也就是说，一个大象细胞，代谢率只有老鼠细胞的1/10。

按照这个规律，如果我的体重增加一倍，我无须吃两倍的食物。因为基础代谢率的下降，我的进食量只需要增加75％就够了。这个规律，适用于所有的哺乳动物、鱼类、鸟类、昆虫，还有细菌和植物。

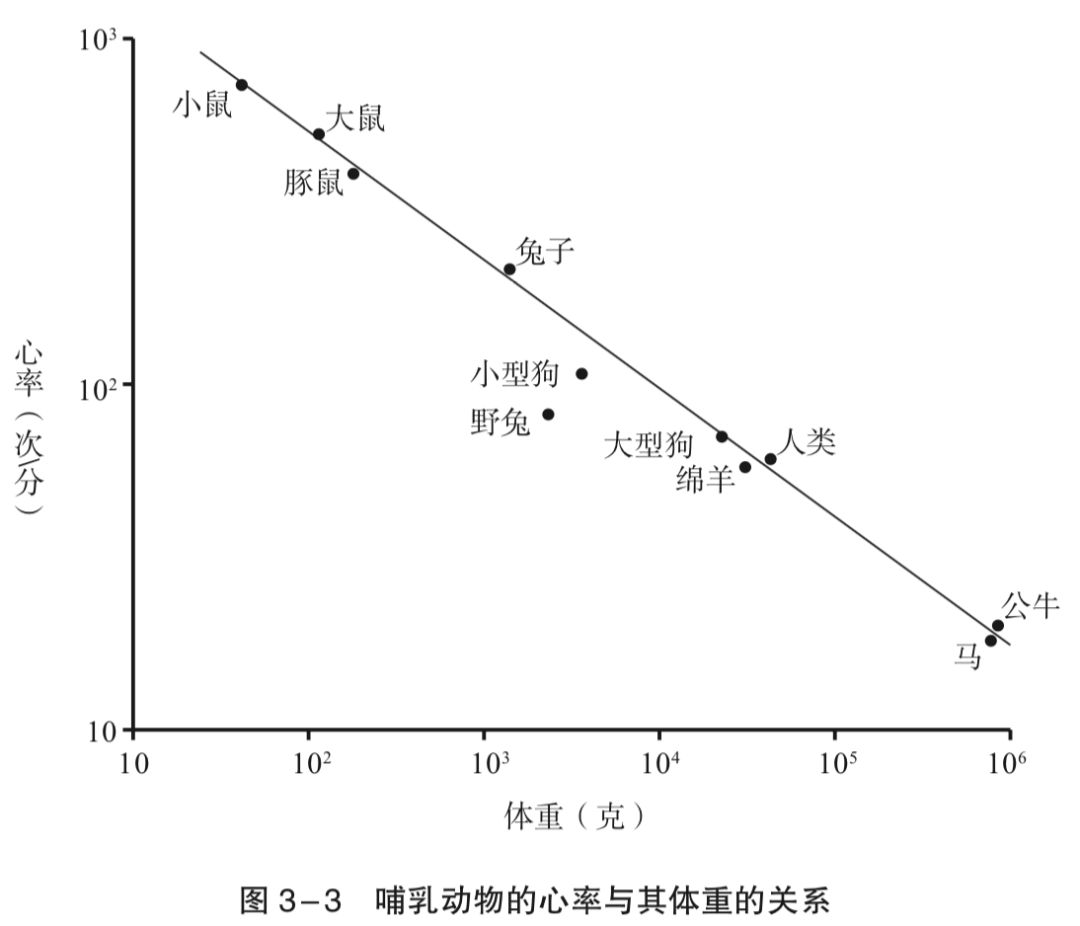
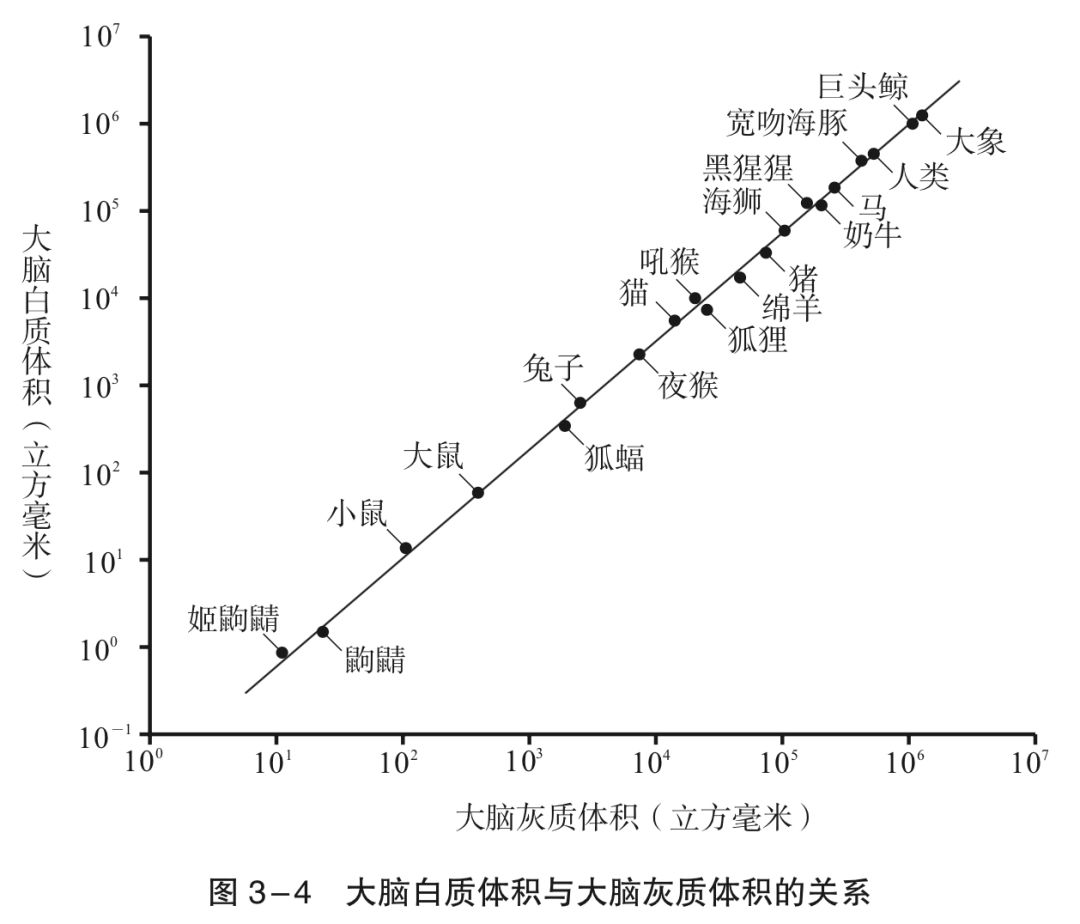
代谢率随着规模的变化而变化，并且这个变化可以被归纳为一个幂函数。韦斯特将之命名为“规模的缩放效应”。在书中，韦斯特罗举了很多例子，向我们说明规模缩放效应在生物界的普遍存在。比如哺乳动物心率与体重的关系、大脑白质与灰质体积的关系、主动脉和气管的半径、呼吸频率、肺泡总面积，以及植物的叶子数、枝条数、枝干半径……“规模每扩大一倍，便会产生25％的节余”的规律无处不在。

写这么一大本书，如果只是阐述90年前的克莱伯定律，那当然不值得。韦斯特这本书的重点在于说明：规模缩放效应不仅存在于生物界，也同样存在于人造的复杂系统，比如城市和公司。因为城市和公司也与生物一样，都满足以下几个特征：

1、个体对异常简单的规则不断重复，便可产生复杂的行为（比如单个蚂蚁行为都非常简单，但整个蚁群的行为却很复杂；再比如个人的买买买，产生了不可预测的宏观经济现象）；

2、整体大于个体的线性之和（构成一个整体的个体之间存在互相作用，导致了复杂的乘数效应，使得整体行为的效用呈现出超线性的特征，并且不可预测，这被称为“涌现”）；

3、对不断变化的外界条件，具有适应和不断变化的能力（从两个人的下棋，到十几亿人口规模的中国对外贸易政策）；

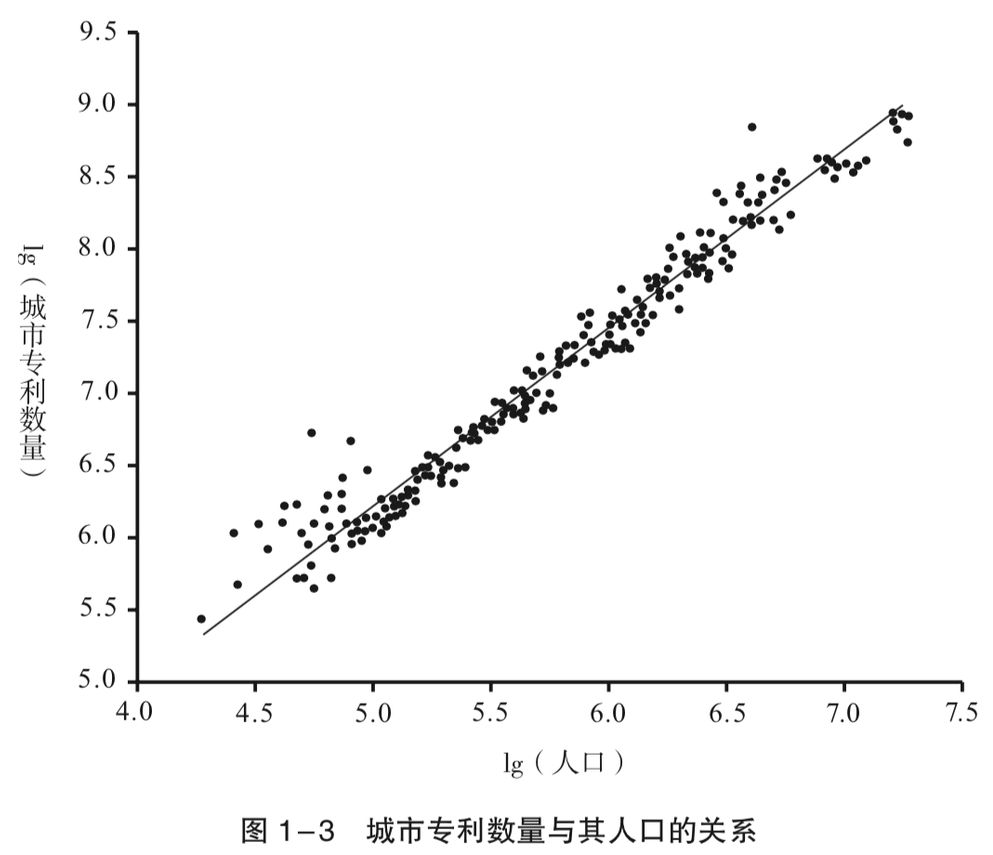
按照韦斯利的统计和总结，城市人口与专利数量、城市人口与自来水管道总长度、公司员工数与净资产……也都存在着规模缩放效应——规模越大，人均耗能越小）不同只在于缩放的指数：如果两只同样大小的熊合体，会节省25％的食物；如果是两个500万人口的城市合并成一个，则可以节省15％的自来水管和道路；而两个同样大小的公司合并，却只能节省10％的费用。

在这本书中，韦斯利在城市这个话题上着墨甚多。原因在于，城市不仅表现出人口规模与基建之间的“节省性”规模缩放效应，也同时存在着增强性的缩放效应。比如大城市人均收入和人均ＧＤＰ的超线性增长，比如大城市人均拥有专利数，都要比小城市和农村的多。也就是说，涉及人与物的关系时，规模效应是指向人均消耗减少的。但是涉及人与人互动时，规模效应是指向人均产出增加的。比如专利，产生于人与人之间想法的交流；收入，则取决于人与人之间的分工协作。

如何理解大城市这种基于人际互动的增强性幂律增加呢？我觉得有这么几个因素吧：

1、人群的聚集，指数级地降低了道路、管线等基础设计的人均成本；

2、人口的规模产生了胖尾——低频的、小众的生意类别（如果我们把艺术视为一类生意的话，它是最好的例子）得以存活。而胖尾的加入，大大丰富了整个城市的商业多样性和层级，其鲁棒性也得到了指数级的提高。就像多物种的亚马逊雨林生态圈比你自家花园更经折腾一样；

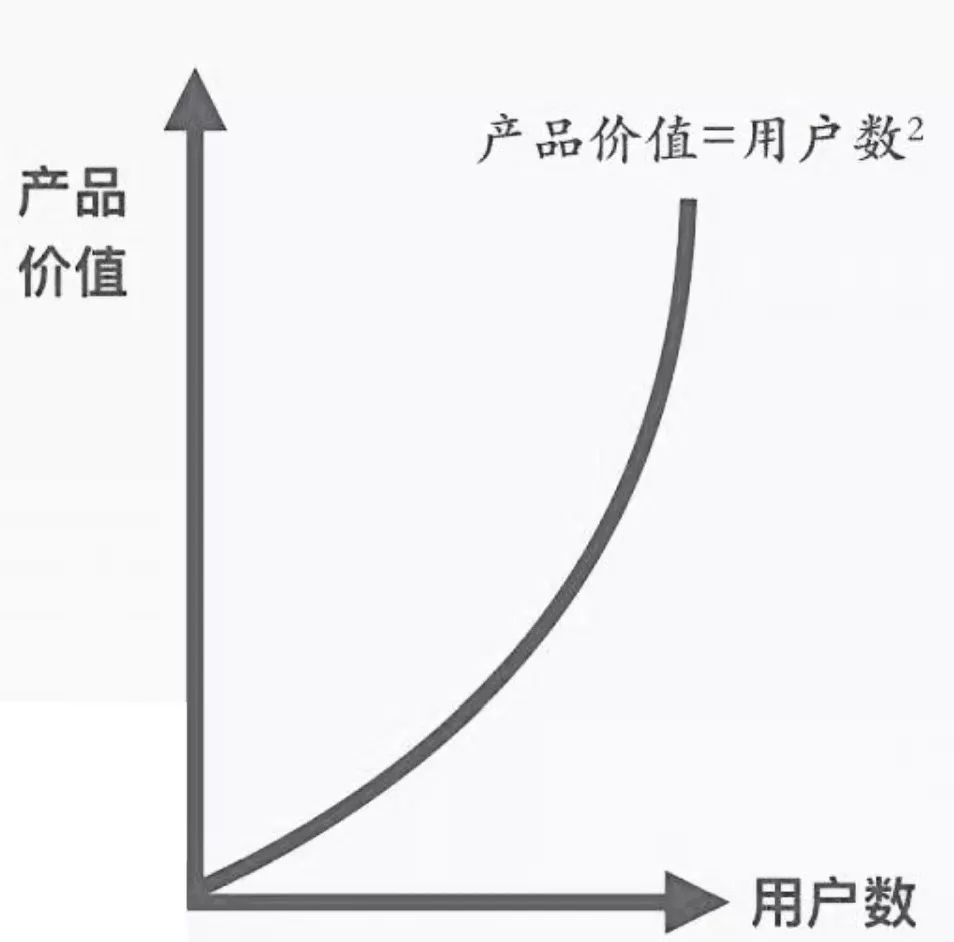
3、了解互联网的人，都知道梅特卡夫定理——一个网站的价值，等于用户数的平方。也就是说，网站的价值＝用户数Ｘ用户间互动的强度。而这个强度，则取决于贴近性。

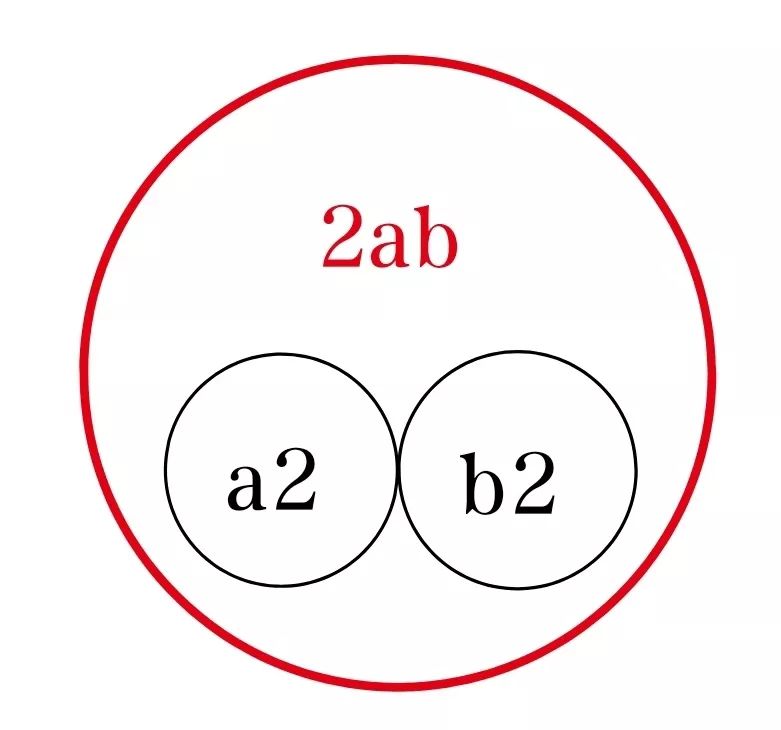
设若有两个网站，其用户数分别为a和b，则按梅特卡夫定理，其各自的价值就分别为a2和b2。那么，如果我们把两个网站合并呢？新网站的用户数为（a+b），其价值为（a+b）2＝a2+2ab+b2。与合并前相比，新网站的价值比合并前两个网站的价值之和，多出了2ab。这就是贴近性的价值所在。

前些年，不知道出于怎样的考虑，我国政府从大力推进城市化的立场，转变为大力进城镇化。“城市化”与“城镇化”一字之差，政策效果却是云泥之别。厉以宁主张在四万个小城镇撒胡椒面，就地消化当地富裕农村人口，以防止人口过于聚集在大城市。真希望他能看到韦斯利的这本书，并动脑子想一想，假如他有的话。

人口的聚集，在达到一定规模之后，会导致生产效率的提高、人均收入的增长和创新范式的加速。这已经是常识。但是随着互联网的曾及，人们产生了这样的疑问：既然大家都是靠互联网沟通，那线下的贴近性是否还那么重要？关于这个问题，《城市的胜利》的作者爱德华·格莱泽和本书作者杰弗里·韦斯特，不约而同地使用了杰文斯悖论，为线下面对面交流的重要性和必要性做了辩护。杰文斯悖论是说：“当燃煤蒸汽机的效率增加、单位煤耗降低后，煤的用量将不降反升。因为用煤更经济了，所以会有更多的人选择用煤”。这个悖论，在互联网时代的人际沟通上也同样适用——基于网络，人们更方便地结识陌生人。社交范围的扩大，催生了更多的线下见面，而不是单纯的替代。互联网越是发达的地区，彼此间的航班就越是繁忙，而不是衰落。也就是说，网络沟通与线下面对面沟通，是彼此促进的正反馈机制，而不是零和的取代关系。

作为一个一流的物理学家，在50岁以后将兴趣转向生物学之后，韦斯特反而达到了他学术生涯的更高峰。他接触各个涉及复杂系统学科的学者，询问他们“你想解决的问题是什么？” “在得到一个正确的生物学问题之后”，理论物理学家杰弗里·韦斯特说，“预测、设计实验、计算和检验，相对就简单了。”这种降维打击的热情和能力，让他当上了圣塔菲研究所的所长。

熟悉圣塔菲研究所的读者都知道，那是关于复杂性研究的耶路撒冷。1984年，同样来自洛斯阿拉莫斯国家实验室的物理学家乔治·考温想出这样一个念头——将各个学科顶尖级的学者聚拢在一起，用物理学的方法研究所有复杂性的问题，亦即：如何给一只草履虫写方程。这个想法，得到了三位诺贝尔奖得主物理学家菲尔·安德森、马瑞·盖尔曼和经济学家肯尼斯·阿罗的积极响应。他们进行的第一个跨学科研究来自于花旗银行的委托。花旗银行的问题是：为什么我们建立了一个包含了4500个公式、可以处理6000个变量的模式，没能预测到贷给第三世界国家的几百亿美金，最终成了坏账？

自成立以来，圣塔菲研究所一直坚持这样的几项原则：

1、聚焦于复杂系统的研究；

2、尽量不设常期研究员，而以研讨会和项目制的方式，延揽各学科最项尖的学者来此短暂聚集；

3、由物理学家担任刺猬，去寻找复杂系统背后简单的、普适的、可以用数学公式表达的规律；而与具备自由意志的对象打交道们的经济学家、生物学家和社会学家们，则至力于让物理学家们理解“对他者的预期”和“对环境的适应”。

AＲ、人工生命、无人驾驶、战胜了柯洁的AlphaGo……基石无不来自于约翰·霍兰德的“基因算法”；布莱恩·阿瑟则在阿罗的支持下，重新绘制了经济学的学科图谱。圣塔菲的学者们，甚至通过与阿克塞尔罗德合作，将自己的智力输出到了政治学领域。而杰弗里·韦斯特关于复杂系统的规模缩放理论，亦可看作中圣塔菲研究所对人类思想领域的又一重量级输出。《自然》杂志将这个理论比喻为“万物生物理论……对生物学的重要性如同牛顿对物理学的贡献”。这或许有一点点言过其实。但是看到如此简单的一个公式能够完美解释这么多复杂的现象，过程中这份智力的享受，让我对作者感激涕零。

我对杰弗里·韦斯特这个老爷子有一份特别的喜欢。他写这本书的时候是75岁，按照他自己的预测，他应该可以活到87岁。他为自己剩下的12年时间列了个愿望表。排在最后一名的愿意是：“这些事情中最难以实现的，就是能看到托特纳姆热刺队赢得英超冠军甚至欧冠了”。我作为利物浦队超过30年的忠实拥趸，实在是觉得有点对不起他了……