地球绕太阳公转，速度是否分秒不差？而公转的轨道是椭圆的，是不是有个什么力在干扰？

开普勒行星运动定律

大约在400年前，开普勒就在天文学家第谷的观察数据基础上总结出了开普勒行星三大定律，其中开普勒第一定律是椭圆定律，指出行星轨道是椭圆的，太阳在椭圆的一个焦点上，这一点题目上说的是对的。

但开普勒第二定律——面积定律指出，行星在椭圆轨道上与太阳连线在相同时间内扫过的面积相等。这表述有点绕，我们看图吧：

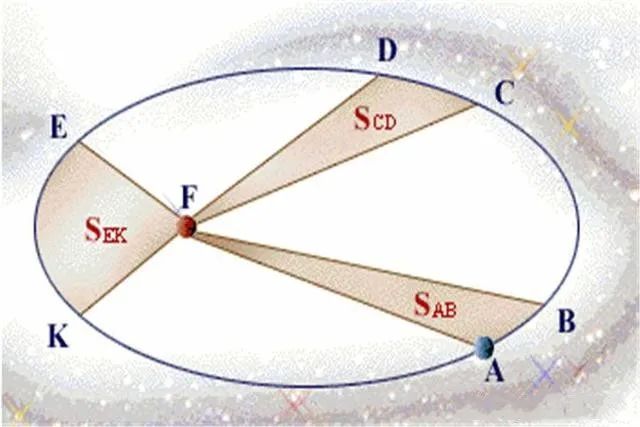
在这个图中，F是太阳，A-B、C-D、E-K就是相同时间内行星公转时经过的距离，而扇形ABF、CDF、EKF就是行星在椭圆轨道上与太阳连线在相同时间内扫过的面积。因此根据开普勒第二定律，A(ABF)=A(CDF)=A(EKF)。

从图中可以很容易看到，AB、CD、EK这三段弧的长度是不一样的，但根据开普勒第二定律，行星经过这三段弧的时间又是相同的，那么只能得出一个结论，行星经过这三段弧的时候的速度是不一样的。行星离太阳越近，公转的速度会越快，反之行星离太阳越远，则公转速度越慢。

什么力拉着地球转？

因此，对于绕椭圆轨道的地球，每时每刻的公转速度都是不一样的，从近日点转向远日点过程中是由快转慢，而由远日点转向近日点的过程中则是由慢转快。所以题目前面的问题就根本不是问题了。不过我们倒是可以讨论一下后面的问题：是什么力引起地球这种公转运动？

这个问题最早由近代物理学之父英国物理学家艾萨克·牛顿给与了解答，他认为行星运动是由彼此间的引力造成的。根据小学语文书的记载，当时牛顿的脑袋被树上掉下来的苹果砸了一下，顿时脑洞大开，领悟了万有引力的奥秘……

由于加入了严谨的数学，牛顿的万有引力理论很成功，在近两百年的时间里解释甚至预言了太阳系行星的运动，在奥本·勒维耶和约翰·柯西·亚当斯分别根据观察数据和万有引力理论计算出海王星位置时，万有引力理论达到了巅峰。

诡异的进动

但很快，随着水星近日点异常进动的发现，观测结果与理论计算不符，牛顿的万有引力理论无法完美解释这一现象。（水星是距离太阳最近的行星，其椭圆轨道的偏心率极高，达到0.2，近日点和远日点距离分别是4600万公里和6981.7万公里，水星在近日点是发生超出牛顿理论预言的进动。所谓近日点进动，就是每次经过近日点时的位置都往前挪了一点。）

爱因斯坦与弯曲的空间

最终解释这一问题的是爱因斯坦的广义相对论。爱因斯坦比较厉害，他不用被苹果砸，单凭一个思想实验就领悟了引力的奥秘。关于这个思想实验具体是什么有不同的传说，有跳楼版，有电梯版，有火箭版，反正蛮穿越的，总之最后领悟了等效原理就对了。

在等效原理下，弯曲的时空呼之欲出了，但要取代牛顿的万有引力理论，数学公式是必不可少的。但爱因斯坦的数学没有牛顿那么NB，他搞了8年才把数学方程搞定，结果一算水星轨道进动，计算结果灰常符合观测值，问题解决。爱因斯坦在广义相对论里，用空间的弯曲代替了引力，行星在弯曲的空间里沿测地线运动，类似于平直空间里沿直线运动。但当我们用平直空间的视角看弯曲空间里行星的运动时，就会误以为它被一个无形的力（引力）拽住做圆周运动。在弯曲空间里不需要这个力，也就是在广义相对论的弯曲空间里，并不存在引力。