距高考还有177天

笔记

PAGE1

双曲线，是中学数学中最重要的曲线之一，但因双曲线的不同表现形式，使得我们在研究这种曲线时，很难准确把握它们之间的内在联系。接下来，我们从最常见的四种不同形式的双曲线，来研究一下“双曲函数”，并尽可能寻找不同双曲函数之间共性的东西，以期让我们对双曲线有更加深刻和不一样的感受。

双曲函数(一)

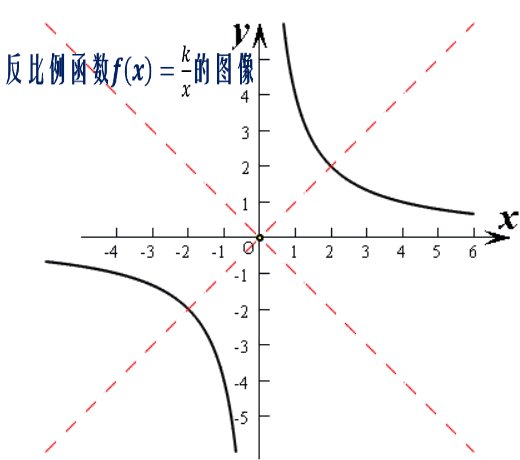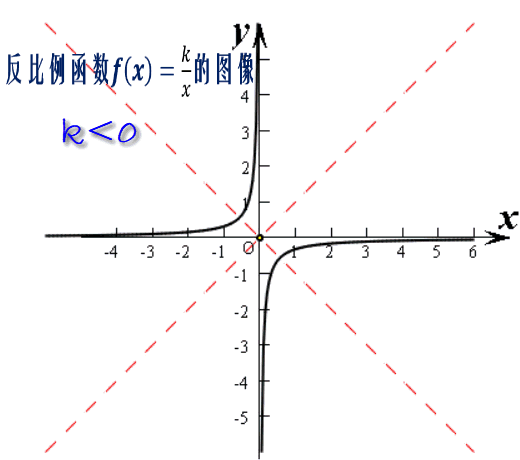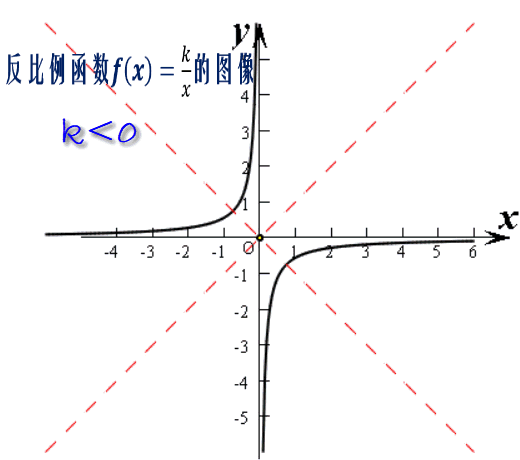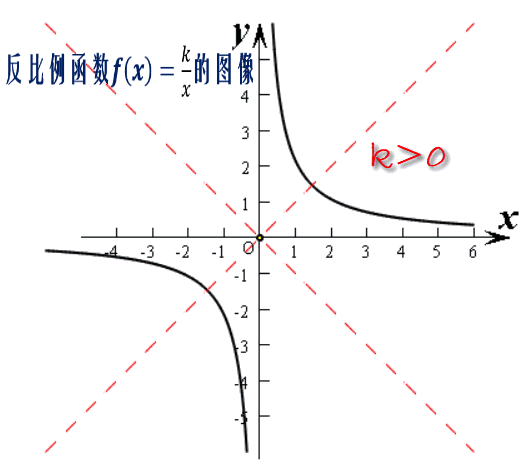
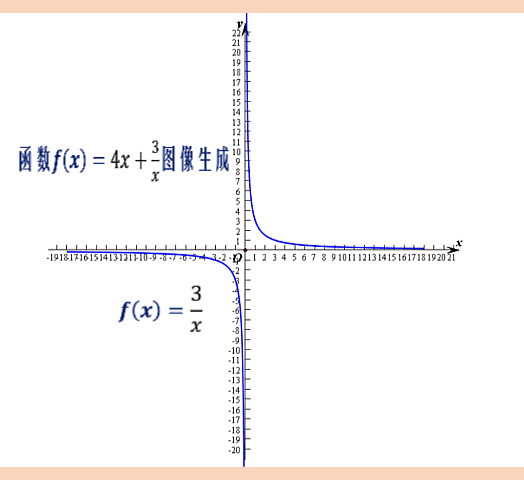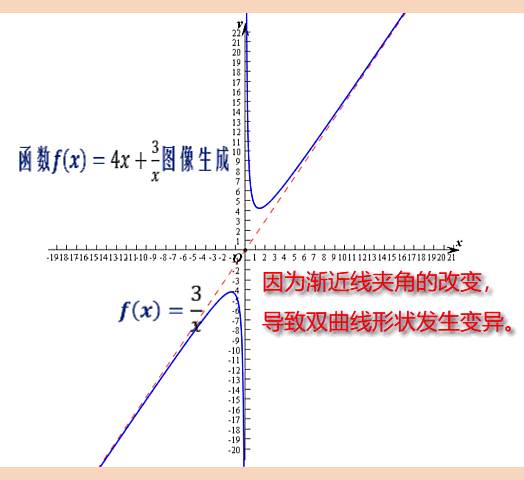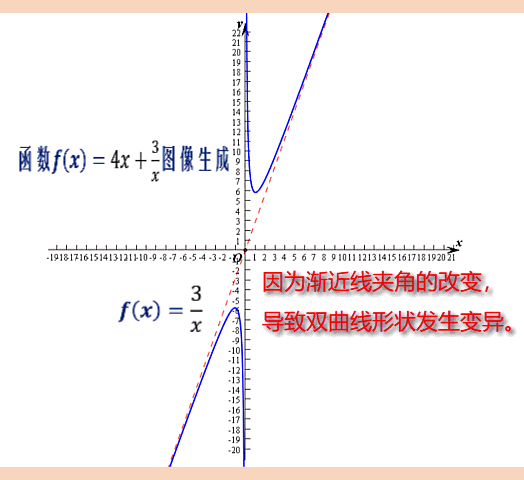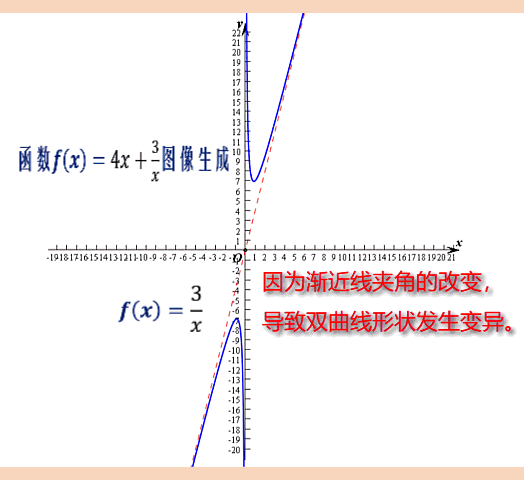
上面这个函数叫反比例函数，应该说，反比例函数是我们接触的第一个双曲函数了，为什么叫双曲函数?主要是因为它的图像是双曲线的原因吧。

“

这个双曲线，既是中心对称图形，又是轴对称图形。 坐标原点是它的对称中心，而直线y=x和y=-x是它的两条对称轴。

最为重要的是，它还有两条渐近线x轴和y轴。

你知道，什么叫渐近线吗?这个双曲线的两条渐近线为什么会是两条坐标轴吗?这两条渐近线又有什么样的性质?

”

渐近线定义

当曲线上一点M沿曲线无限远离原点或无限接近间断点时，如果M到一条直线的距离无限趋近于零，那么这条直线称为这条曲线的渐近线。

根据渐近线的位置，可将渐近线分为三类： 水平渐近线、垂直渐近线、斜渐近线。

其实，曲线的这种特征，我们一般称为收敛。

双曲函数(二)

应该说，形如这种形式的函数，是我们平时接触较多的吧，其实，研究这种函数还是比较简单的，因为它通过裂项(部分分式的化简)后，一定是这个样子的：

所以，它一定是由某个反比例函数的图像经平移而得到的。

就象是下面这个函数：

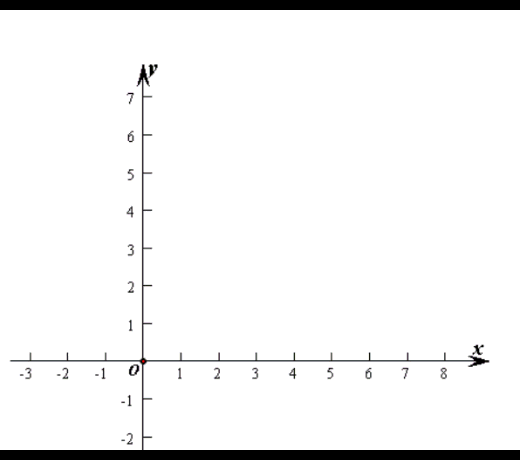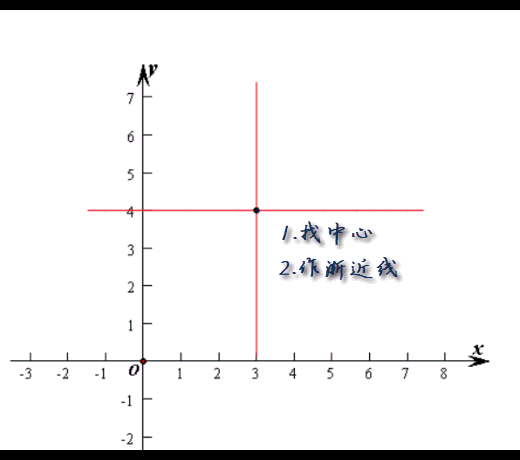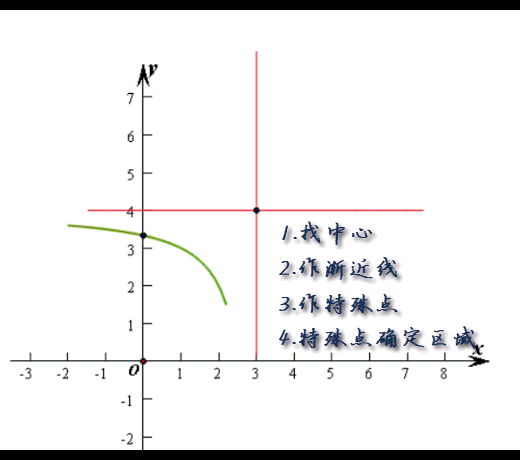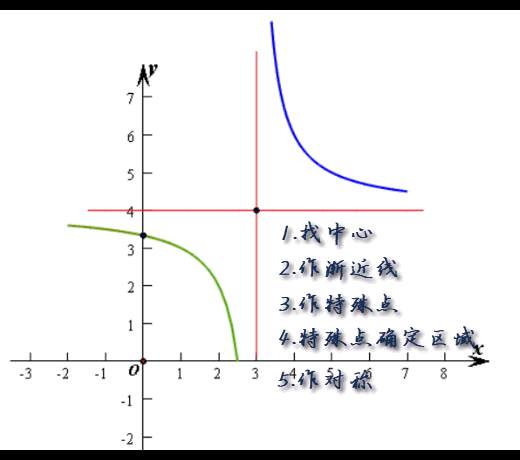
其实，对于这个函数，如果认定了其图像是双曲线，我们以后是可以用稍简便的方法进行作图的。

因为x≠3,且当x→3时,f(x)→∞,所以x=3为一条渐近线，又y≠4,故y=4为其一条渐近线，双曲线中心为点(3,4)，

具体的作图过程是下面这个样子：

双曲函数(三)

这个函数，应该是我们在中学阶段最常见的函数了，当a、b同号时，因其形状象极了老师给我们批阅作业所用的√，所以老师们喜欢叫它“对勾函数”。

其实，它也是一种类似于反比例函数的双曲函数，由图像得名，又被称为

“双勾函数”

“勾函数”

"对号函数"

“双飞燕函数”

因函数图像和耐克商标相似，也被形象称为

“耐克函数”或“耐克曲线”。

总是，是很多人都喜欢的函数了。

从上面的图像可以看出，对勾函数与反比例函数图像的区别，好象只因为渐近线的夹角发生了变化，导致双曲线发生扭曲，从而不再具备轴对称的特征而已。

对勾函数渐近线的理解：

当x→∞时,f(x)→ax,所以y=ax为渐近线； 又x→0时,f(x)→±∞故x=0时（即y轴）为其第二条渐近线。

当a,b异号时，曲线的渐近线依然为y轴和y=ax,但此时y轴左右两侧，函数均为单调，相对来说，降低了研究的难度。

02

此时的曲线，依然为扭曲的双曲线。

双曲“函数”(四)

其实，我们都知道，这个已经不能称之为函数了。

但在解析几何中，它的图像我们明确称作“双曲线”。

当a=b时，我们称双曲线为等轴双曲线，此时两条渐近线互相垂直，就与反比例函数所对应当的双曲线有着极深的关系了。

“

那我们其实可以这样说，解析几何中的等轴双曲线，其实就是反比例函数图像绕原点旋转45度得到的，

因此，在反比例函数中，也应该有焦距和实轴的概念了，你也可以试着去求一下吧。

”

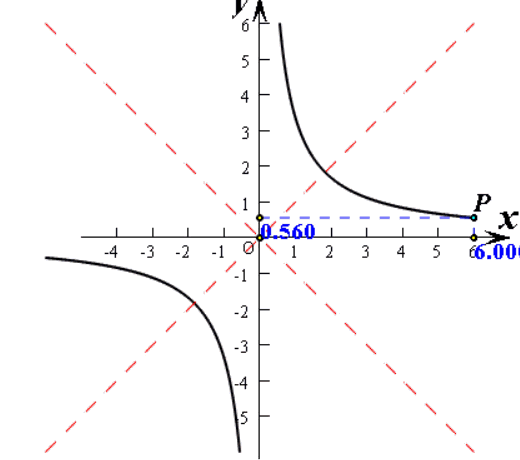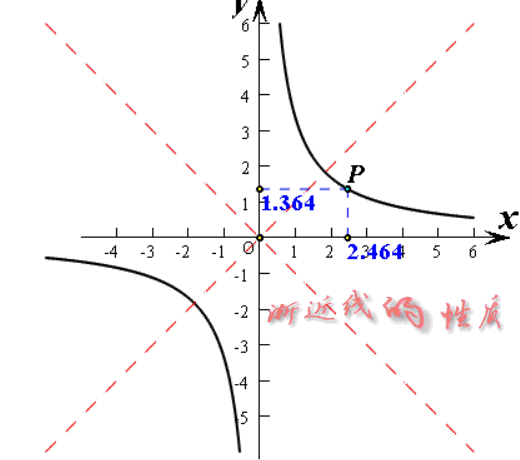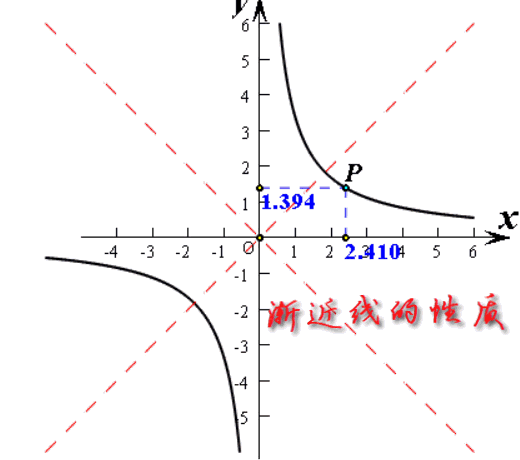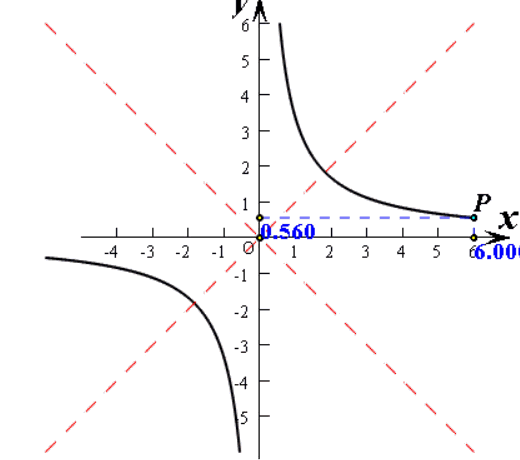
其实，从上面对几个常见双曲函数的分析可以看出，要规范双曲线的形状，其实至关重要的是渐近线，而且不同的双曲函数中，渐近线好象都有一个共同的性质，那就是曲线上任意一点到渐近线的距离之积总是定值的。

当然，对于解析几何中的双曲线来说，还有很多其它的知识，需要我们去补充，比如准线及定义，都是非常重要的。