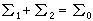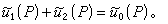在光的衍射中，结构互补的一对衍射屏，在同一场点所产生的两个衍射场(复振幅)之和，等于自由传播时该点的光场。巴俾涅原理给出两个互补屏产生的衍射场之关系称巴俾涅关系，它可由衍射积分公式直接导出。

如图，设孔型屏Σ1造成的衍射场为ũ1(P)，其互补屏Σ2造成的衍射场为ũ2(P)，而光波通行无阻Σ0面的光场为ũ0(P)，则 ，

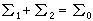
故

因此，只要两个互补屏的照明条件不变，对后场任意一点，不论是近场点还是远场点，巴俾涅关系都是成立的。

巴俾涅原理的价值在于，一旦已经求得某屏的衍射场，利用巴俾涅原理便可求得其互补屏的衍射场，这是因为自由光场ũ0(P)总是容易事先知道的。

据此，知道了圆孔的衍射场，就能方便地求得圆屏的衍射场；知道了单缝的衍射场，就能方便地求得细丝的衍射场；诸如此类。巴俾涅原理用来处理夫琅和费衍射问题特别有效，因为此时的自由光场除几何像点外处处为零，所以这些地方的场ũ1(P)=-ũ2(P)，衍射强度I1(P)=I2(P)，而在几何像点处，两个互补屏的衍射光强应该都是亮点，但光强值可能不同。

因此，两个互补屏的夫琅和费衍射图样看起来完全相同。需要强调指出：巴俾涅原理给出的三个场之关系是复振幅关系，其中位相差要起作用而不是三者光强之关系，不能认为一屏的衍射强度在某处若是亮的，互补屏的衍射强度在该处一定是暗的。 

关注 ©中国大百科全书数据库了解更多