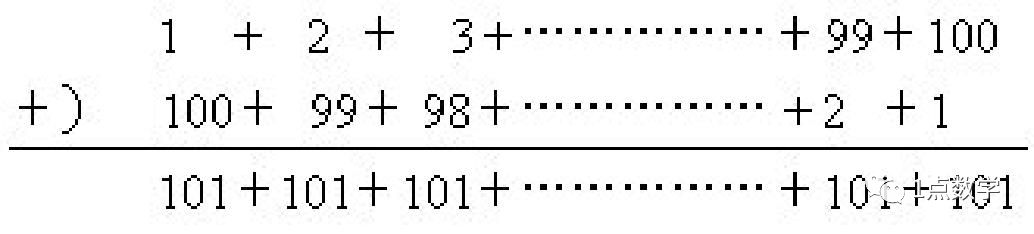高斯和小行星的发现
高斯(Carl Friedrich Gauss) 1777年4月30日生于德国的布伦兹维克(Braunschweig),1855年2月23日卒于格廷根(Gottingen),是近代数学伟大的奠基者之一。他在历史上影响之大,可以和阿基米德、牛顿、欧拉并列。

高斯出生在一个贫苦的家庭里,祖父是农民,父亲做短工,舅舅腓特烈(Friederich)是一个很有才能的入,自已学会了纺织技术,很快成为一个出色的锦缎织工。他经常教给高斯一些知识,对幼年的高斯影响很大.
高斯父亲本不打算让他上学,但高斯很小就显出有数学才能。一个星期六的晚上,他父亲计算工薪帐目,没注意到小高斯在旁边看着.他算了半天才完,不料高斯说:“爸爸,你算错了,应该是.....”核对一下,果然是高斯说得对,父亲又惊又喜,七岁的时候,决定送他上学.
高斯10岁的时候,数学教师布特纳(Bittner)要求学生将100个数相加起米,这100个数恰好成等差数列(如1 +2+3 +...+100之类),刚解释完题目,高斯就把有答案的石板交上去。布特纳连看也没看,心想这个全班最小的学生准是瞎写了些什么或者交了白卷。过了很久,别的学生才一个个把石板叠在上面。等到布特纳发现高斯的石板上只写着一个正确的答案,而比他大的孩子都算错了的时候,才大吃一惊。在这以前,他从未教过学生计算等差数列。
有经验的布特纳立刻意识到这是一件不寻常的事。他买了一木最好的算术书送给高斯,并说:“他已超过我,我已经没有什么可以教他的了。”
高斯仍然留在小学里,教师的助手巴特尔斯(Johann Martin Bartels, 1769--1836)是一个好学的十七岁青年,他同高斯一起学习了很多数学。巴特尔斯后来主持喀山大学的数学讲座,著名的罗巴契夫斯基是他的学生。
由于巴特尔斯的推荐,高斯得到一个公爵的资助,在1795年进了格廷根大学。
1796年高斯(19岁)发现正十七边的尺规作图法,这是欧几里得以来悬而未决的问题,为了纪念这个发现,格廷根大学在高斯去世后,为他建立了一个以正十七边形棱柱为底座的纪念像。
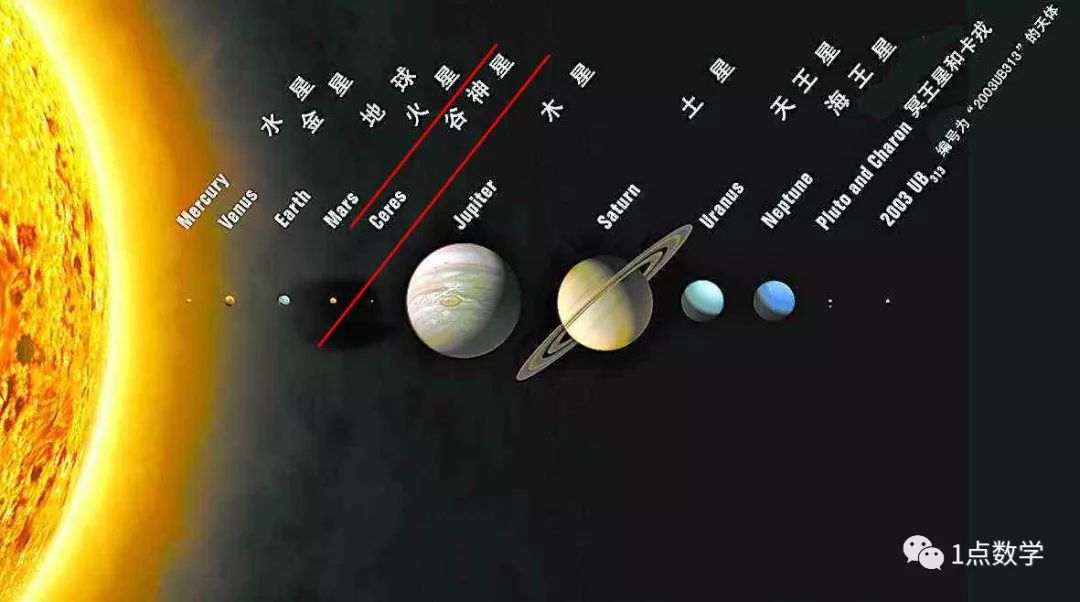
1781年以前,入们只知道有五大行星:水、金、火、木、上,1766年提替斯(J.D.Titius, 1729--1796)总结出这样的经验公式:设地球与太阳的平均距离(即一个天文单位)是10,那么各行星与太阳的距离是:
水星4=4+0 (3.9)
金星7=4+3 (7.2)
地球10=4+6 (10)
火星16=4+12 (15.2)
(?) 28=4+24 (?)
木星52= 4 +48 (52.0)
土星100=4+96 (95.4)
括号内是是实际距离,它和左边计算出来的数字很接近,左边的数字是用数列0,3, 6,12,……加上4得出来的,这数列减去第4后,每一项都是前一项的2倍。
1772年德国天文学家波德(Johann Elert Bode, 1747.1.19--1826.11.23,柏林天文台台长)加以整理后发表,现在叫做“波德定律”。
这一简单关系虽然是数字的凑合,没有理论根据,但还是引起了天文学家的极大注意。大家都认为在相当于28那个空档里,可能有一个未发现的行星。
1781年3月13日赫歇耳(Frederick William Herschel,1738. 11.15--1822.8.25)发现土星之外还有一个行星,以后定名为天王星。它和太阳的距离是192,和波德定律的计算结果196很接近。这更加强了寻找新行星的信心和决心。但辛辛苦苦找了二十年都没有结果,却在一次偶然的观测中发现了,正是:踏破铁鞋无觅处,得来全不费功夫。
19世纪的第一个晚上(1801.1.1),皮亚齐(Giuseppe Piazzi, 1746.7. 16--1826.7.22)在意大利西西里岛的巴勒莫(Palermo)天文台为了核对星图,观察金牛座一带的星,偶然看到一颗8等星和星图不合。第二夜发现已向西移动,他以为这是一个没有尾巴的彗星。连续观测了四十天,一直到2月11日,终于因为劳累过度病倒了。
他将观测结果写信告诉欧洲大陆的天文学家,那时正值拿破仑远征埃及,英国舰队封锁了地中海。直到1801年9月,大陆上的天文学家才知道这件事,引起很大的震动。但那时这颗星已被阳光所掩,无法寻找,似乎它已在无数群星之间永远消逝了.
于是产生一个难题,怎样根据极有限的观测数据来确定新行星的轨道?当时许多著名的天文学家都着手解决这个问题,但都失败了。
孙悟空十万八千里的筋斗,跳不过如来佛的手心,行星的怪异运动,也终于逃不出数学家的掌握。24岁的高斯,经过几星期的努力,克服了种种困难,创立了行星椭圆轨道法,成功地解决了这个问题。这导致一个8次方程。
另一个天文学家查赫(Baron von Zach, 1754--1832)根据高斯的方法,造了一个觅星表,预报这颗星的位置。可是天公不作美,连日阴雨,无法观测。直到这一年的除夕,天气大睛,天文学家在预测的位置上,重新找到了这颗星。这是科学的辉煌胜利,它显示了数学理论的巨大威力。
这颗星定名为谷神星(Ceres),与太阳距离27.7,和波德定律大致相符.然而事情还没有结束,谷神星的直径只有770公里,是地球的6%,木星的0. 55%,在火星与木星之间,大小太不相称。
以后又在这个空隙里陆续发现了许多小星,这些星现在叫做小行星,被发现的小行星的数目越来越多,最初用神的名字命名,神的名字不够用,就用人名、国名等来命名。目前正式编号的已达两千颗之多。
高斯后来总结了这种方法,写成《天体沿圆锥曲线绕日运动的理论》(Theoria motus corporum coelestium in sectionibus conicis solem ambientium, 1809)。在这书中他首次叙述了最小二乘法原理。这对测量学有重要意义,高斯是大地测量卓越的理论家和实践者。
高斯对电磁学、光学的贡献并不亚于天文学和大地测量。1833年他和韦伯(Wilhelm Eduard Weber, 1804. 10.24--1891.6.23)共同发明了电磁电报,后来为了纪念高斯,磁通量密度的单位以高斯命名。
1827年高斯出版《曲面的一般研究》(Disquisitiones generales circa superficies curvas) ,继欧拉、蒙日之后将微分几何大大推进一步,并决定了这一学科发展的基本方向。
高斯在1816年左右就得到非欧几何的原理,但他从未发表过这方面的著作。高斯知多言少,他一生虽然发表了155篇论文,但还有大量创作没有发表出来,例如他曾深入研究了复变函数,发现解析函数沿闭曲线的积分为0,但没有发表。后来为柯西重新得到。
高斯总是等到作品十分成熟的时侯才公布出来。呈现在人们面前的只是完美无瑕的结果,而省略了分析和思考的过程,一般的学者很难掌握他的思想方法。
有些学者对于高斯的过份拘谨有些看法。他们认为如果具有洞察力的高斯及早发表他的真知灼见,对后辈会有更大的启发,进入新的领域也就更快.
在纯粹数学方面,高斯对数论最感兴趣。他在19岁时就发现并证明了二次互反律(quadratic reciprocity law) .这是他的得意杰作,称之为“黄金律”,(theorema aureum),一生曾用八种方法去证明它。高斯的数论研究总结在《算术探究》(Disquisitiones Arithmeticae, 1801) 中。这书奠定了近代数论的基础,它不但是数论方面的划时代著作,而且可以列为历史上最有代表性的数学著作之一。
高斯曾说:“数学是科学之王,数论是数学之王(Mathematics is the queen of the sciences and arithmetic the queen of mathematics)。它常常屈尊去为天文学和其它自然科学效劳,但在所有的关系中,它都堪称第一。”
前两句话常被引用,第一句是容易解释的,第二句仅仅说明高斯对数论的偏爱。
本文完~
如果看到了这里,那就点个赞分享一下吧^_^