让人类随机说出一个1-10之间的整数(包括1和10),每个数字被选中的概率都是10%吗?答案当然是否定的。
半年前,有人对8500名学生做了一项调查,发现人类似乎对7有种特殊的偏好,有接近3成的人会选择“7”,而选择两端数字的概率会偏小,选“10”人甚至仅有1.9%。
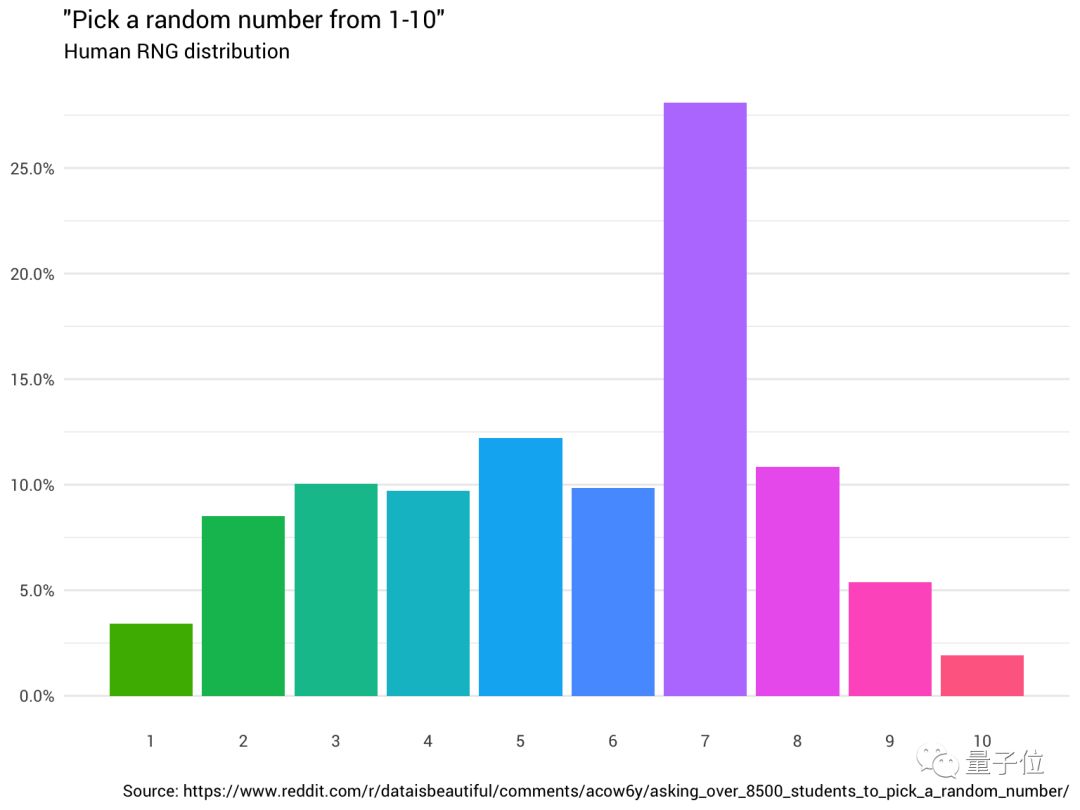
如果用计算机,我们就可以生成近乎完全随机的数,保证每个数被抽中的概率都是10%。(注:其实计算机生成的是伪随机数,并不完全随机,但效果远胜过人类。)
在这件看似超级简单的事情上,人脑输给了电脑。人类随机函数human.random远不及Numpy里的np.random啊。
难怪有Twitter网友会调侃:智人诞生30多万年以来就没能解决这个问题。
因为人类是有情感的:1和10分别位于两端,选择这样两个数是否会太刻意?7是不是我的幸运数字?潜意识里的想法都会左右你最终的选择。
那该怎么办?
怎么才能把人类随机函数变成真正的随机函数,要做的就是把概率分布大于10%的数挪到概率小于10%的数上。
你可以想象成切碎这些长条并重新排列,让它们都一样高:
举一个极端的例子,假设我们将每个长条都“切割”成无限小的块,然后就可以像乐高一样使用这些块来建立任何形状的概率分布。
现在,我们来定义这样一个变量xi,j,它表示我们把数字i调整到数字j的样本占数字i总样本中的比例。
因为选7的人比较多,我们希望把部分7调整到1,如果把20%的7变成1,那么x7,1=0.2。xi,i表示自身不调整的部分。
最后我们希望所有随机数的概率都是0.1,所以其他数字调整进j的比例之和应该满足:
同时,我们还必须确保原始分布中的所有概率质量(probability mass)都是守恒的。所以每个i调整到1到10的总概率应该等于1(注:原文如此,应等于原本选择数字i的概率Pi)。
另外,我们还希望尽可能保留原始的分布,也就是让xi,i(保持不动的部分)之和最大,即不调整的部分尽可能多。
现在这个问题就变成了一个线性规划问题,在这20个约束条件下,令对角元素之和最大。
经过电脑计算后,调整方案是这样的:
这个结果虽然直观却不够精确,准确的调整比例为:
按照上面的图表,选7的结果中有28%的比例需要调整为10,20%的比例需要调整为1,等等。
但是这28%、20%的比例如何获得,最初的随机分布表就可以啊。
本来就有28%的人选择7,如果我们获得了一个7,在问第二个人,如果也得到一个7,我们就把第一个7强制转换成1。
人脑随机数生成器
现在你明白人类随机数生成器的工作原理了,下面就是这套程序的“源代码
向一个人问得1~10之间的随机整数n1;
if n1=5
then 再向另一个人问得一个随机整数n2;if n2=5 (概率12.2%)then 返回随机数 2;if n2=10 (概率1.9%)then 返回随机数 4;else 返回随机数 5;if n1=7then 再向另一个人问得一个随机整数n2;if n2=2或5(概率20.7%)then 返回随机数 1;if n2=8或9 (概率16.2%)then 返回随机数 9;if n2=7(概率28.1%)then 返回随机数 10else 返回随机数 7;if n1=8then 再向另一个人问得一个随机整数n2;if n2=2 (概率8.5%)then 返回随机数 1;else 返回随机数 8;else 返回随机数 n1;
按照这个程序,你应该能得到一个接近平均的从1到10的随机数发生器,前提是你得有8500个人。









