投掷小针的实验

十八世纪某日，法国博物学家布丰（Comte de Buffon）邀请了许多朋友来家中做客，席间一起做了个实验。布丰先在桌上铺好一张大白纸，白纸上画满了等距离的平行线，再拿出很多等长的小针，小针的长度刚好是相邻平行线间距的一半。布丰说：「请大家随意把这些小针往白纸上扔！」客人们纷纷照他所说的做。

用火柴重复布丰实验

他们总共投掷了二千二百一十二枚小针。统计结果表明，与纸上平行线相交的有七百零四枚，2210÷704≈3.142。布丰说：「这是 π 的近似值。每次实验都会得到圆周率的近似值，而且投掷次数愈多，求出的圆周率近似值就愈精确。」这就是著名的「布丰实验」。

布丰发现，如果选用的小针长度固定，那麽有利扔出（扔出的针与平行线相交）与不利扔出（扔出的针与平行线不相交）的次数之比，就是一个包含 π 的运算式。特别的是，如果小针的长度是平行线距离的一半，那麽有利扔出的概率恰好为 1/π。

布丰投针问题的实验数据

下面是利用这个公式，用概率法获得圆周率近似值的历史资料。

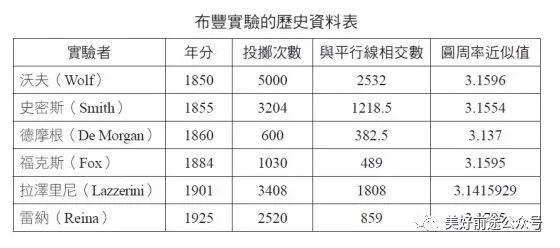
布丰实验的历史资料表

其中，义大利人拉泽里尼在一九○一年投针三千四百零八次后，得出的圆周率近似值为 3.1415929，精确到小数点后六位。只不过他的实验资料遭到了美国犹他州韦伯州立大学的巴杰教授的质疑。但无论如何，透过几何、概率、微积分等不同领域和多种管道均可求取 π 的值，这仍然令人惊讶。

布丰投针实验是第一个用几何方式来表达概率问题的例子，也是首次利用随机实验来处理确定性的数学问题，它推动和促进了概率论的发展。

布丰投针问题的证明

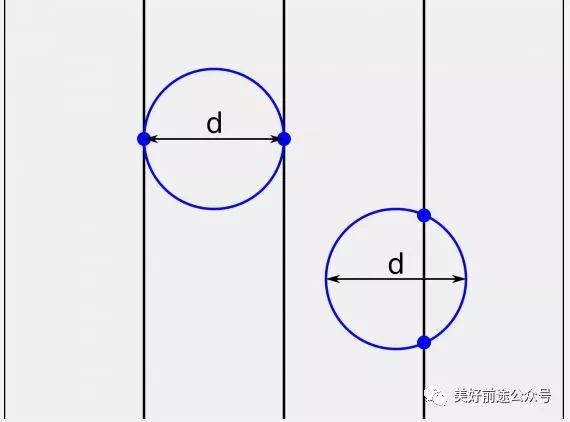
找一根铁丝做成圆圈，使其直径恰好等于两条平行线的间距 d。不难想像，对于这样的圆圈来说，不管怎麽扔，都会与平行线有两个交点。这两个交点可能在一条平行线上，也可能在两条平行线上。因此，如果投掷圆圈的次数为 n，那麽交点总数必为 2n。

现在把圆圈打开，变成一根长度为 πd 的铁丝。显然，这根铁丝投掷后与平行线相交的情形要比圆圈複杂，共有五种情况：四个交点，三个交点，两个交点，一个交点，无交点。

一个圆圈的直径等于平行线之间是 d，不论怎麽仍都会与平行线有两个交点

由于圆圈和直线的长度同为 πd，根据机会均等原理，当投掷较多次且投掷次数相等时，两者与平行线交点的总期望值应该是一样的。也就是说，当长度为 πd 的铁丝被投掷 n 次时，与平行线的交点总数也应该约为 2n。

现在来讨论铁丝长度为 l 的情形。随著投掷次数 n 的增加，铁丝与平行线的交点总数 m 应当与长度 l 成正比，因而有 m=kl，其中 k 是比例係数。

为了求出 k，考虑到当 l=πd 时的特殊情形，有 m=2n。由此可得

特别地，取 l=d/2，便可得到布丰的结果，即 m/n=1/π。这个证明多多少少比较直观，若学了高等数学，还可以用概率论和微积分的方法提出更严格的证明。

有趣的是，布丰的名字与义大利尤文图斯守门员兼义大利足球队队长布冯的名字拼法相同，均为 Buffon，只不过前者是法国人，后者是义大利人；前者生活在十八世纪，后者则与我们同年代。

布丰，身兼多职的皇家植物园园长

布丰出生于盛产美酒的勃艮第小官吏之家，母亲颇有人文修养。他十六岁时前往第戎的学院读书，虽然喜欢数学，却不得不遵从父命学习法律。此番经历与他的同龄人、瑞士数学家欧拉相似，那会儿欧拉在离第戎不远的巴塞尔大学，听从父亲之意攻读神学和希伯来语。

原因在于，对于非显贵家庭出身的年轻人来说，牧师、医生和律师不失为安身立命的三个好职业，欧拉却偏偏对数学情有独锺。

欧拉二十岁时隻身前往俄国的圣彼得堡科学院，先在医学部，后来转到数理学部，凭藉自己的钻研和努力，成为十七世纪最伟大的数学家，也被誉为历史上最伟大的四位数学家之一。布丰同样是在二十一岁时，转往法国西部的昂热大学攻读医学、植物学和数学，并结识了一位在欧洲大陆旅行的英国公爵，陪他去了不少地方，也多次随他前往英国，后来还成为英国皇家学会会员。

法国博物学家布丰

二十五岁时，布丰的母亲去世，他回到故乡经营自家农场。他经常去巴黎，是文学和哲学沙龙的常客，并结识了伏尔泰等知识分子，自己也著作等身。他认为，写作能力包括思想、感觉和表达，内心的明晰，味觉和灵魂。布丰在四十六岁那年当选为法兰西学院院士，就像二十世纪的数学天才庞加莱（Henri Poincaré），同时站在科学与人文两大领域的顶峰。

布丰三十二岁时被任命为巴黎皇家植物园园长，直到去世都担任此职。他致力于把植物园办成学术和研究中心，从世界各地购买或获取新的植物和动物标本。布丰翻译过英国植物学家黑尔斯（Stephen Hales，第一个测量血压的人）的《植物志》（Vegetable Staticks）和牛顿的《流数法与无穷级数》（Methodus Fluxionum et Serierum Infinitarum），并探索了牛顿和莱布尼茨发现微积分的历史过程。布丰还主编巨著《自然史》，原计画出五十卷，在他去世前出了三十六卷。

布丰生前以博物学家的身份和自然史方面的著作闻名，并以「风格即人」的理念为人称道和传世。这就像北宋的政治家沉括，因为写了《梦溪笔谈》而被公认是伟大的博物学家，在数学、物理学、地质学等方面同样卓有成就。布丰的兴趣也非常广泛，且在多个领域均有重要建树。

布丰是最早提出要将地质史按照时期划分，并发表太阳与彗星碰撞产生行星此一理论的人。他还率先提出物种绝迹说，促进了古生物学的研究。不过，他说新世界（指美洲）的物种之所以不如欧亚大陆，缺乏大型和强大物种，男子气概的人也少于欧洲，是因为美洲大陆沼泽的气味和茂密的森林，大大激怒了汤玛斯．杰佛逊（Thomas Jefferson），派出二十个士兵去新罕布夏州森林寻找公鹿，好向布丰展示「美国四足动物的雄壮和威严」。

布丰四十五岁时娶了一位来自故乡没落贵族世家的小姐，他们的第二个孩子倖免夭折，五年后却面临母丧，布丰又在他八岁时病重，幸好隔年病情就好转，从此父子平安无事。布丰后来活到八十一岁，晚年当选为美国艺术与科学学院的外籍院士。

蒙地卡罗方法是什麽？

如同前文提到的布丰投针试验，透过概率实验的方法来估计某一个随机变数的期望值，这样的方法被称为蒙地卡罗方法。

蒙地卡罗全景

蒙地卡罗是全球驰名的赌城，位于法国国界内离义大利不远的摩纳哥，傍依地中海海滨，属于风景如画的「蔚蓝海岸」一部分。奥斯卡电影《蝴蝶梦》曾在这裡取景，一级方程式赛车在这裡也设有一站。我年轻时游历此地，发现它与美国的拉斯维加斯和大西洋城不同，要求客人西装革履，穿短裤或拖鞋者谢绝入内。

蒙地卡罗方法是美国在二战期间执行研製原子弹的「曼哈顿计画」时提出来的，主要归功于波兰人乌拉姆（Stanislaw Ulam）和匈牙利人冯．诺依曼这两位犹太籍数学家。冯．诺依曼以赌城蒙地卡罗之名为此方法命名，也为它罩上了一层神祕面纱。其实在此之前，蒙地卡罗方法就已存在，比如布丰实验。

如今，蒙地卡罗方法在原子物理学、固态物理学、化学、生态学、社会学与经济行为学等领域均获得广泛应用。下面，我们再举两个例子。

例一：把布丰实验做个推广，利用钝角三角形的边长计算圆周率。

三角形

任意给三个正数，以它们为边长，可以围成一个钝角三角形的概率 P 也与 π有关，这个概率为(π–2)/4。证明如下：

设这三个正数为 x、y、z，而且 x≦y≦z。对于每一个确定的 z，考虑到一个三角形任意一边的长度小于另外两边的长度之和，故满足

x+y>z, x2+y2

后一个不等式成立是因为钝角三角形和毕氏定理。我们很容易证明，这两个不等式即为以这三个正数为边长可围成钝角三角形的充分必要条件。

因此，满足假设条件的（x, y）的可行区域为直线x+y=z 与圆 x2+y2

由此可见，这个概率与 z 的选取无关。因此，对于任意正数 x、y、z，均有 P=(π–2)/4，命题得证。

为了估算 π 的值，我们得透过实验来估计其概率，过程可交由电脑程式设计来实现。事实上，x+y>z，x2+y2

若进行了 m 次随机实验，有 n 次满足该不等式，那麽当 m 够大时，n/m 会趋近于 (π–2)/4。而若令 n/m=(π–2)/4，可求得 π=4n/m+2，由此即能估计出 π 的近似值。

例二：利用蒙地卡罗方法，求任意曲边梯形的池塘面积。

蒙地卡罗方法的基本概念是：先建立一个概率模型，使所求问题的解正好是该模型的参数或其他相关的特徵量。再透过模拟某个统计实验，即多次随机抽样实验（确定 m 和n），统计出该事件发生的百分比。只要实验次数够多，该百分比便近似于事件发生的概率，这其实就是概率的统计学定义。

可以说，蒙地卡罗方法属于实验数学的一种。它的适用范围很广泛，既能求解确定性的问题，也能求解随机性的问题，甚至可以探索科学研究中的理论问题。

例二告诉我们，如何利用蒙地卡罗方法近似计算定积分，这属于数值积分问题。那麽，任意曲边梯形形状的池塘面积，应该怎样测算呢？

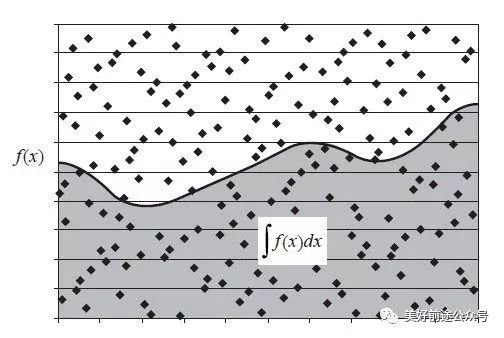
设计方案是：如下图所示，假定池塘位于一块面积已知的矩形农田中央，随机朝农田扔泥巴，泥巴可能会溅起水花（落在池塘内），也可能不会（落在池塘外）。估计「溅起水花」的泥巴数占总泥巴数的百分比，便可根据该比例和农田面积近似算出池塘的面积。

用蒙地卡罗方法计算曲边梯形的池塘面积