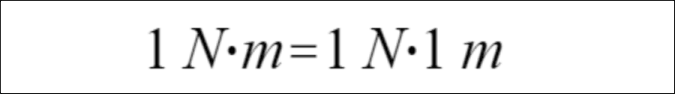文 | 嗷嗷胡

千万别羞赧，相信我，某些几十上百万粉丝的汽车大V，假如你突袭式提问“什么是扭矩”，现场回答也多半是支支吾吾、含含糊糊、企图蒙混过关。

什么是扭矩、马力、功率，这一类问题是被无数先辈们翻来覆去，炒过足足八百遍的文物级陈年冷饭了。然而讲真，我看过无数号称零门槛科普，最终也没发现一篇浅显到能让物理零分学渣（no offense）直呼“搜打死内”的。

但偏偏，这几个词对于任何汽车相关的从业者、消费者乃至吃瓜人，都属于抬头不见低头见，避不开的老熟人。前两年特斯拉发布Roadster2和Cybertruck时，动辄上万牛·米的“轮上扭矩”给大伙吓懵逼，除非有人给你解释：这个轮上扭矩啊，它不是你以为的那个扭矩……

此扭，非彼扭

圆周运动的马甲

我愿赌五毛钱，你一定刷到过“加速看马力还是看扭矩”这样的滥大街问题&回答。不论你是否点进去看了，无论你点进去是否看懂了，走过路过很难错过。

对于扭矩这类正常人看见就打瞌睡的物理词汇，这确实大概是最抓眼球的讨论姿势，车迷们看到就来劲儿。因为人们都很容易落入一个思维模式：非要把问题简单化总结化，是A还是B？A重要还是B重要？由A决定还是B决定？

但最吸引人的，不一定就是最有用的。具体到我们的问题，更符合人脑认知逻辑的是先搞明白“扭矩/马力/功率各自是什么”，自然而然你就会明白“加速由谁决定”等等衍生问题。相反，假如你前面零基础就直接接触后者，多半这俩问题会一起难住你很久。

确实这可比物理课刺激多了……

我们之所以先从扭矩（Torque）说起，是因为扭矩你可以理解为，它是功率的两个“来源”或“组成”之一。扭矩的计量单位是牛·米/N·m，中间的点表示乘号，这个点有时会被省略。

“扭矩”加上“牛·米”这个单位，看上去仿佛很高深，其实没必要自己唬自己。所谓扭矩，不过就是我们再熟悉不过的“力”——唯一使它显得故作高深的是，这个力是旋转的力，而非高中物理常见的直线力。

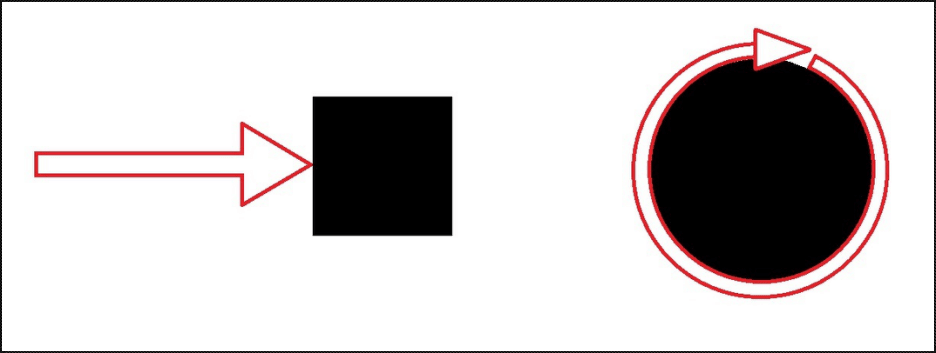
不信你瞧瞧人家隔壁火箭发动机，输出的是直线推力，于是描述火箭发动机的推力直接用“xxxx吨”、“xxxx牛”就行了，一目了然。

直线力很简单，哪怕文科生也都能轻易理解，比如朝这边推是+10牛，朝反方向推是-10牛嘛。但汽车行驶是靠轮子，驱动车轮的力是旋转力，这样情况就稍稍复杂了，因为旋转力不像直线力那么方便量化。

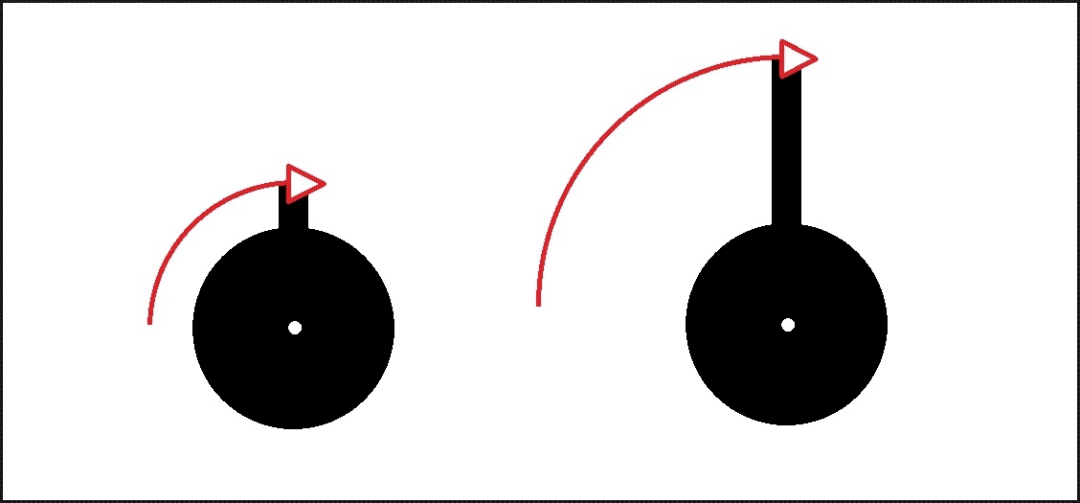
同样的一个旋转物体，在离旋转轴心不同距离/半径处，表现出的力的大小一定是不同的。

杠杆效应各位都懂：越是离轴心近/半径小，对外表现出的力越大；离轴心越远/半径大，对外表现出的力越小——但实际上，那个使物体旋转的力，并没有变。

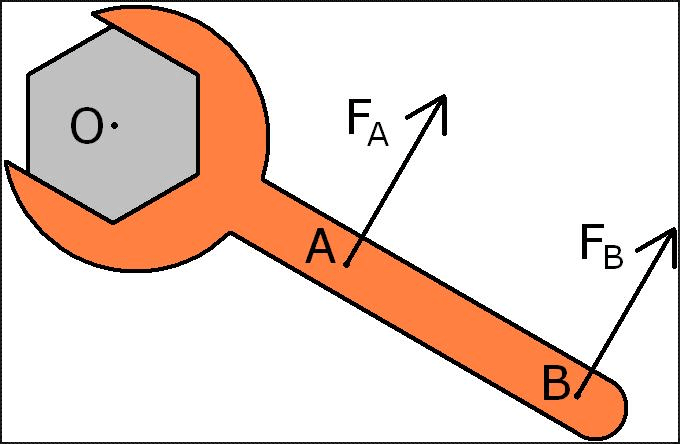
反过来，杠杆定理告诉我们，要给一个物体施加某个大小的旋转力，可以在离轴心较近的位置（小半径）施加较大的力，也可以在离轴心较远的位置（大半径）施以较小的力。只要力和力臂的乘积相同，二者最终的效果是完全一致的。

力臂OA×力Fa=力臂OB×力Fb

于是问题来了：对于一个旋转的力，“xx牛”无法确定其大小。

比方说，假如我们说一个旋转的力是“10牛”，怎么知道是在离轴心/半径0.5米处是10牛？还是在离轴心/半径1米处是10牛呢？反过来，是在离轴心0.5米处施加10牛的力，这个旋转力算“10牛”？还是在离轴心1米处施加10牛的力，这个旋转力算“10牛”呢？

说不清了这就。

直线力的单位“xx牛”不行，但力与力臂的乘积却可以。

因为根据杠杆定理，只要力与力臂的乘积是同一个定值，那么对于杠杆中心施加的作用效果就是相同的。既然描述直线力的“xx牛”无法描述一个旋转的力，我们借来杠杆定理公式，取力与力臂的乘积，作为旋转力的计量单位。

于是，就有了这个看上去好复杂、好高级、好难懂的扭矩单位，“牛·米/N·m”——其实不过是“牛/N”的“旋转版本”。很多人对扭矩不理解，罪魁祸首就是这个奇怪的单位。但恰恰是，如果结合“牛·米/N·m”这个单位，对于扭矩理解起来反而更容易一些。

在离旋转物体轴心/半径1米处，施以1牛顿大小的力，作用于这个物体的旋转力即为1牛·米；反之同理，在1牛·米的旋转力作用下，离旋转轴心1米半径处，力的大小为1牛顿。

所谓扭矩、牛·米，其实就这么点事儿，无非是旋转力需要一些额外骚操作罢了。

浦东就是上海

扭矩说穿了就是力，只不过这个力在转圈，功率则是更进了一个层级。

单纯的“力”其实毫无意义，因为再大的力，也需要作用距离才能有实际效果。哪怕你全身憋足了力量，但拳头一毫米都不动杵那儿杵着，那杀伤力也是零，除非是在金庸小说里。

要衡量力“干了多少活儿”，人类确立了“功”的概念：用力的大小乘以力作用的距离。功代表一个总量，那么要评判“出活儿的效率”，可以用这个总量除以花掉的时间，即功率=功/时间。又因为总量=速度×时间，可以得到功率=力（的大小）×（力作用下的）速度。

其实就和打工差不多……工作量、时间、工作效率

再回到现实中去理解，当我们谈论车“快不快”时，说的其实是单位时间内做功的多少，即“做功的效率”。“功”用来描述一个总量，“功率”则是描述一个效率。效率越高，动力越强；效率越低，动力越差——很像打工人的日常是不是。

再将“发动机输出旋转力”套进去，扭矩只表示单纯的“（旋转）力的大小”，而这个力需要作用一段距离才有实际效果（功）；这个实际效果除以花了多少时间，得到的就是“单位时间内干的活儿”，即出活儿效率（功率）。

或者，还是利用总量=转速×时间，直接用力的大小（扭矩）乘以力的作用速度（转速），也可以得到功率。

说到这，该请出一个公式：功率（kW）=扭矩（N·m）*转速（RPM）/9549。

这个公式的推导过程不必细说，虽然你可能看着眼晕，但其实无非是角度弧度、速度时间的互相转化罢了——属于“我虽然看不懂但我知道我不是真的看不懂”型知识。“9549”是精确到个位的近似数，后面原本带着一串无限不循环小数，由将圆周运动角速度转化为线速度时除以π而得。

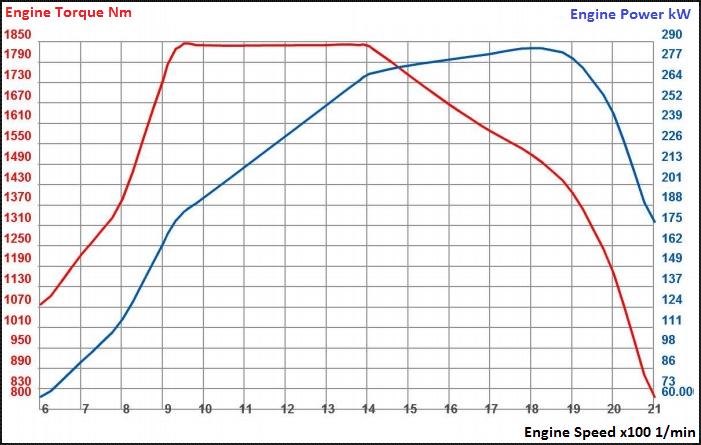
9549是个恒定常数，所以，功率与扭矩转速之乘积是直接相关的。我们平时看到的那些发动机功率-扭矩图，其实功率曲线上任何一点的功率千瓦数，都可以通过该点对应的扭矩、转速之乘积，再除以这个常数9549而得到。

甚至，功率本来就是一个无法直接测量得到的数据。发动机功率曲线，是在台架上测得扭矩与实时转速，再经过计算才得到的。常见的功率-扭矩图，其实只要给出扭矩曲线，功率曲线我们自己就能手算然后画出来，毕竟转速就在下面坐标轴上摆着呢。

所以不妨这么说：扭矩“就是”功率（的一部分），因为功率由扭矩和转速相乘得到。二者相伴而生，零扭矩高速空转的发动机，是无功率可言的；只要转速不变或增加，更高的扭矩一定意味着更高的功率。

世间万物皆杠杆

回到扭矩本身，你其实很容易找出一个bug：很多汽车发动机的扭矩不过100-200N·m，按照上面的理解，相当于在发动机输出轴装个1米长的把手，在把手上施以100牛也就是10千克的力——这几乎是个成年人都能做到。

一方面，这样的力就足以驱动一两吨重的车飞奔吗？一方面，一台发动机燃烧汽油做功，结果就这？

要回答第一个问题，首先需要明确：燃油车世界说到的“扭矩”，指的皆是“曲轴扭矩”，即发动机输出轴上力的大小。发动机后面有什么？变速箱，主减速器，差速器。在低挡位，变速箱会将发动机动辄几千转的转速降低数倍，再经主减速器，最终到车轮上的转速可以被降低十几倍。

功率并没有变（不计传动损耗），而转速被降低了。根据功率=扭矩×转速（*常数），轮端的转速被降了多少倍，轮端的扭矩就会提升多少倍——这就是所谓的“轮上扭矩”。

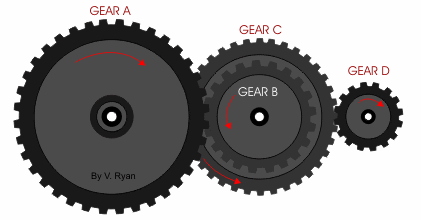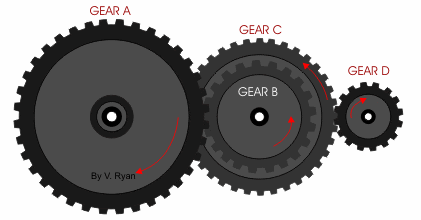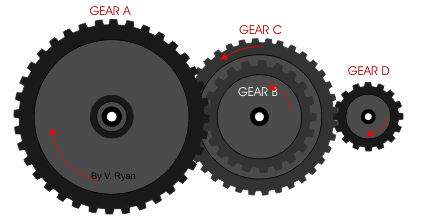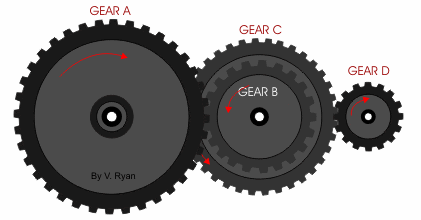
抛开数学公式，实际中也好理解：用小齿轮去带动大齿轮，转速会变慢，但力量被放大。代价则是需要转过更多的圈数，才能跑完原先的行程。齿轮传动本也符合杠杆原理，被放大的力量来自更长的行程，二者的乘积始终不变——正如扭矩与转速乘积也始终是定值（功率不变）。

动力稍微靠谱的乘用车，在一挡时的轮上扭矩都可以达到5000-10000牛·米，所以说特斯拉的10000牛·米轮上扭矩，是一个走信息不对称路线的营销话术。并且，轮端扭矩其实与车辆动力性能并不直接相关，而是与偏好设定更紧密。比如硬派越野车很多可以轻松越过10000N·m——无非把减速齿轮做得更大一些罢了，根本就没有啥成本。

几千上万牛·米的轮上扭矩，才是真正驱动车辆跑起来的那个力。

至于第二个问题，为何一台汽油发动机轰轰烈烈就搞出这么10千克的力呢？别忘了还有个转速在那儿。发动机并不仅仅是产生一个“1米半径处10千克的力”，还能以最高每分钟几千转的频率持续产生这样的力——这可就不是哪个人类能做到的了。

所以说汽油燃烧机械运转的结果，不光是产生了一个100-200N·m的静态扭矩（力），更带动着发动机活动部件以动辄数千转/分高速运转，最终是以每分钟几千转的频率持续产生100-200N·m的扭矩。

扭矩和功率，差不多是汽车动力性能最最核心、也最最基本的参数。如果不理解扭矩和功率的含义和关系，对于动力性能更细节、更深层的认识，就很容易受到局限乃至误导。而一旦掌握了这个基本知识，对于理解车辆动力系统会有很大帮助——不限于燃油车或电动车。

扭矩是理解所有动力话题的基础，无论是“加速看哪个”这样的市井老题，还是正确理解响应等动力特性、梳理引擎技术发展脉络、评判电机与燃油机的不同等等。如果不理解扭矩的含义和与其他参数间的关系，也许不影响你对汽车的了解和爱好，但终将停留在浅尝辄止，更别谈形成自己的主观判断。

其实呢，扭矩无非就是个力，可别被一个圆周运动附带的唬人单位给吓跑了。