串联电路的三个原理：

电流：通过串联电路中任何组件的电流量相同。

电阻：任何串联电路的总电阻等于各个电阻的总和。

电压：串联电路中的电源电压等于各个压降之和。

让我们看一些演示这些原理的串联电路示例，我们将从包含三个电阻器和一个电池的串联电路开始：

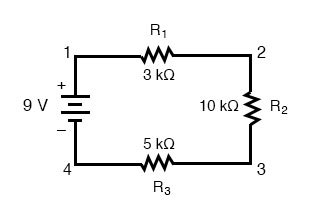
了解串联电路的第一个原理如下：

串联电路中通过任何组件的电流量都是相同的。这是因为串联电路中只有一条电流路径。由于电荷流过管中的大理石之类的导体，因此电路（管）中任何特定时间点上的任何点的流速（大理石速度）必须相等。

在串联电路中使用欧姆定律：

从9伏电池的排列方式可以看出，该电路中的电流将沿顺时针方向流动，从点1到2到3到4再回到1。但是，我们有一个电压源和一个三个抵抗。我们在这里如何使用欧姆定律？欧姆定律的一个重要警告是，所有量（电压，电流，电阻和功率）必须根据电路中的相同两个点相互关联。我们可以在下面的单电阻器电路示例中看到这个概念的实际作用。

在简单的单电阻电路中使用欧姆定律：

使用单电池单电阻电路，我们可以轻松地计算任何数量，因为它们都应用于电路中的相同两点：

由于点1和点2与电阻值可以忽略不计的导线连接在一起，点3和点4一样，我们可以说点1与点2在电气上是公共的，点3与点4在电气上是公共的。在点1和点4之间（直接跨电池）有9伏的电动势，并且由于点2是点1共有，点3是点4共同，我们也必须在点2和3之间有9伏（直接跨电池）电阻）。

因此，我们可以将欧姆定律（I = E / R）应用于流经电阻的电流，因为我们知道电阻两端的电压（E）和该电阻的电阻（R）。所有项（E，I，R）都适用于电路中相同的两个点，也适用于相同的电阻，因此我们可以毫无保留地使用欧姆定律公式。

在具有多个电阻器的电路中使用欧姆定律：

在包含多个电阻器的电路中，我们必须谨慎应用欧姆定律。在下面的三电阻示例电路中，我们知道点1和点4之间有9伏，这是通过R 1，R 2和R 3的串联组合驱动电流的电动势。但是，我们无法将9伏的值除以3k，10k或5kΩ来尝试找到电流值，因为我们不知道这些电阻器中的任何一个电阻的电压分别是多少。

9伏特的数字是整个电路的总数量，而3k，10k和5kΩ的数字是单个电阻器的单独数量。如果我们将总电压的数字与单个电阻的数字插入欧姆定律方程中，则结果将与实际电路中的任何数量都不准确相关。

对于R 1，欧姆定律将涉及R两端的电压量1通过R的电流1，给定的R 1的电阻，的3kΩ：

但是，由于我们不知道R 1两端的电压（只有电池在三电阻串联组合上的总电压），而且我们不知道流过R 1的电流，因此无法进行任何计算任一个公式。R 2和R 3也是如此：当且仅当所有项代表电路中相同两点之间的各自量时，我们才能应用欧姆定律方程。

所以，我们能做些什么？我们知道在R 1，R 2和R 3的串联组合上施加的电源电压（9伏），并且我们知道每个电阻的电阻，但是由于这些量不在同一环境中，因此我们可以不要使用欧姆定律来确定电路电流。如果只有我们知道的总电阻是为电路：那么我们就可以计算出总有我们的身影当前总电压（I = E / R）。

将多个电阻器组合成等效的总电阻器，这将我们带到串联电路的第二个原理：任何串联电路的总电阻等于各个电阻之和。这应该具有直观的意义：电流必须流过的串联电阻越多，电流流动就越困难。在示例问题中，我们有一个串联的3kΩ，10kΩ和5kΩ电阻，使我们的总电阻为18kΩ：

本质上，我们已经计算了R 1，R 2和R 3的等效电阻。知道了这一点，我们可以使用一个等效电阻来重绘电路，该等效电阻代表R 1，R 2和R 3的串联组合：

使用欧姆定律计算电路电流：

现在我们有了计算电路电流所需的所有必要信息，因为我们在点1和点4之间有电压（9伏），在点1和点4之间有电阻（18kΩ）：

使用欧姆定律计算组件电压：

知道串联电路中所有组件的电流相等（并且我们刚刚确定了流过电池的电流），我们可以返回到原始电路原理图并记下流经每个组件的电流：

现在我们知道通过每个电阻的电流量，我们可以使用欧姆定律确定每个电阻两端的电压降（在适当的情况下应用欧姆定律）：

注意每个电阻两端的电压降，以及电压降的总和（1.5 + 5 + 2.5）如何等于电池（电源）电压：9伏。

这是串联电路的第三个原理：串联电路中的电源电压等于各个电压降之和，用“表法”和欧姆定律分析简单串联电路

但是，可以简化我们刚刚用来分析此简单串联电路的方法，以便更好地理解。通过使用表格列出电路中的所有电压，电流和电阻，可以很容易地看出在任何欧姆定律方程中哪些可以正确关联：

此类表格的规则是仅将欧姆定律应用于每个垂直列中的值。例如，E R1仅具有I R1和R 1；仅E R2和I R2和R 2 ; 等等。首先，您需要从一开始就填写表格中的那些元素来开始分析：

从数据的排列中可以看出，我们无法将9伏ET（总电压）应用于任何欧姆定律公式中的任何电阻（R 1，R 2或R 3），因为它们是在不同的列中。9伏电池电压未直接施加在R 1，R 2或R 3上。但是，我们可以使用串联电路的“规则”来填充水平行上的空白点。在这种情况下，我们可以使用电阻的串联规则从各个电阻的总和中确定总电阻：

现在，在总电阻值插入最右边（“总”）列的情况下，我们可以将I = E / R的欧姆定律应用于总电压和总电阻，以得到500 µA的总电流：

然后，知道电流被串联电路的所有组件（串联电路的另一个“规则”）平均分配，我们可以从刚刚计算出的电流图中为每个电阻器填充电流：

最后，我们可以使用欧姆定律来确定每个电阻两端的电压降，一次确定一列：