上一期 不公平的选择

现在桌面上有一副洗过的扑克，52张，背面朝上。你和另一人参加博弈。

主持人会一张张翻开扑克。

连续三张牌的颜色序列——如黑黑黑、黑红黑之类——就是所博弈的结果。

你与对手各押注一个获胜序列——如红红黑和黑红红——出现在先。当然，押对了的人获胜。

现在是这样，你获得了一个选择的机会：先押或后押。大家认为哪个更有利？

若你的对手优选选择了后押，则你必须先提出自己的获胜序列，大家能找到相对有利的序列吗？

可能有些朋友一时没有想清楚，为何后手可以占据大优势。这里举一个最简单的例子，如果先手选择致胜序列为000，则后手简单地选100。

此时，若先手在最开始的前三张里没有开出000，那他就已经输了。因为若之后某n位置上第一次三连开出000。但既然

这是第一次出现000序列，则第n-1个位置必然是1，所以从n-1开始的连续三张牌为100。后手胜。

对一般的结论，评论区 鱼鱼鱼葱卷 指出

留意到先手选好行后，后手总可以对应地选列，让先手胜率小于 0.5，可见后手占优。

如果对手是后手，我就要将行中最小值最大化，换言之选“红黑红”或者“黑红黑”，最优先手策略的胜率是 0.334776。

下表行号对应先手，列号对应后手

----- 0.500 0.398 0.393 0.118 0.413 0.287 0.500

0.500 ----- 0.665 0.671 0.245 0.627 0.500 0.713

0.602 0.335 ----- 0.500 0.496 0.500 0.373 0.587

0.607 0.329 0.500 ----- 0.500 0.504 0.755 0.882

0.882 0.755 0.504 0.500 ----- 0.500 0.329 0.607

0.587 0.373 0.500 0.496 0.500 ----- 0.335 0.602

0.713 0.500 0.627 0.245 0.671 0.665 ----- 0.500

0.500 0.287 0.413 0.118 0.393 0.398 0.500 -----

最优先手策略的胜率是 0.334776。

刚上初中的小明用一块边长一分米的正方抹布擦桌子。桌子是边长4分米的正方形。

小明突然想到一个问题。

如果抹布不褶不皱，就是一块正方形不变形。此外，它初始位置是桌子的左上角，且边时刻与对应的桌子边保持平行。现在如果用它抹过桌子的全部点，那抹布的几何中心走过的距离是多少呢？

如果桌子边长是2分米或3分米，我们知道答案分别是3和8分米。

但对4分米的桌子，你能想出移动距离小于15分米的擦法吗？

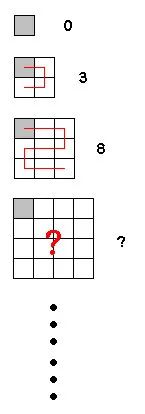
如果觉得初中题太简单，可以试试5分米的情况~

感谢none