自UMAP问世,论文作图使用t-distributed Stochastic Neighbor Embedding(tSNE)还是Uniform Manifold Approximation and Projection(UMAP)的问题一直存在。本文将围绕tSNE和UMAP的算法逻辑、特点差异及应用要点进行介绍。相信各位阅读过这篇文章后对tSNE和UMAP的选择和使用会有自己的判断。
一、tSNE和UMAP算法概要
不同于PCA、LDA等线性降维方法,tSNE和UMAP可以直接将高维空间的结构特征投影到低维空间(二维、三维)中。通俗地讲,就是用平面或立体空间内的点的疏密远近表现其在原本多维度状态下的疏密远近。降维过程如图1所示。

图1. tSNE和UMAP的算法共性
虽然tSNE和UMAP在算法的总体思路上相似,但每一步又有所区别。其中最重要的有两点,一是计算高维距离时,tSNE会计算所有点之间的距离,通过Perplexity(困惑度)参数调整全局结构与局部结构间的软边界,而UMAP则只计算各点与最近k个点之间的距离,严格限制局部的范围;另一方面,两种算法在对信息损失的计算方法不同,tSNE使用KL散度衡量信息损失,在全局结构上存在失真的可能,而UMAP使用二元交叉熵,全局和局部结构均有保留。(表1展示了tSNE和UMAP较重要的算法差异。)
表1. tSNE和UMAP的算法差异
二、降维效果差异及原因
(一)全局结构
在用tSNE降维单细胞数据时,经常会发现同一类细胞被其他细胞分隔。这是因为其损失函数(KL散度)对低维近、高维远的惩罚较轻,导致在平面上,整体差异较小的集群(cluster)可能比差异较大的集群离得更远。故而tSNE图多数情况下不能体现真实的全局结构。
UMAP损失函数使用的是二元交叉熵,对低维近高维远或低维远高维近的惩罚都较重,所以UMAP比tSNE更能体现真实的全局结构。
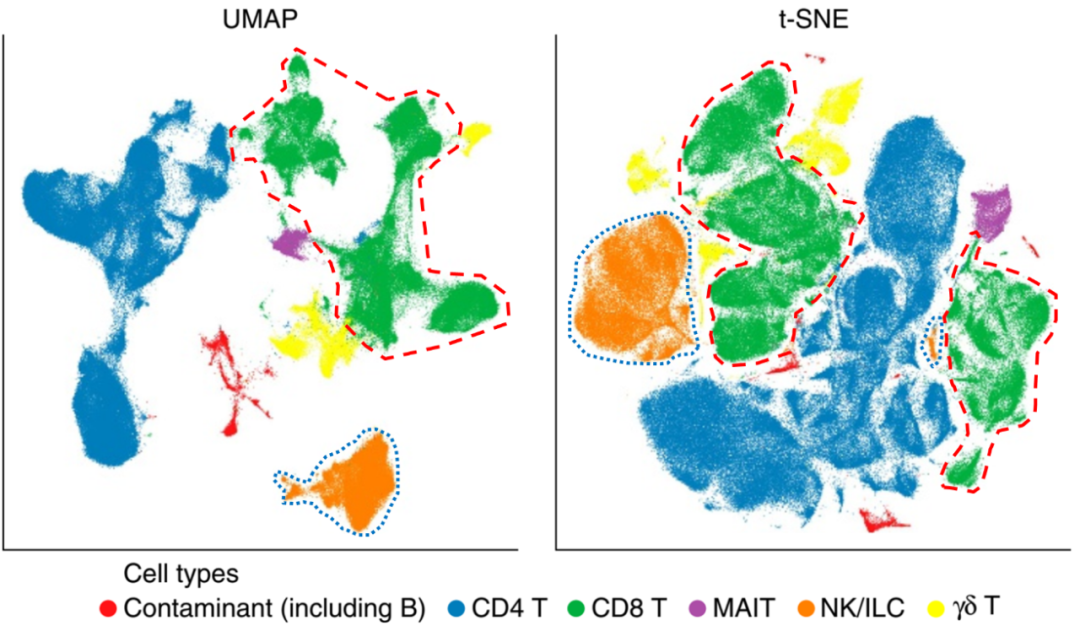
图2. CD8+ T细胞(绿色点)在tSNE中被分散到两个区域,且中间间隔了CD4+ T细胞(蓝色点),而在UMAP图中能很好地聚在一起。此外,NK/ILC细胞(橙色)从两个区域聚成一个,γδ T细胞(黄色)、污染(红色)分布的区域也更集中
图3. KL散度的惩罚分数是不对称的,X(高维距离)小、Y(低维距离)大时罚分高,X大Y小时罚分趋近于0,而二元交叉熵(CE)罚分则是对称的,无论X大Y小还是X小Y大,均有较高罚分。
(二)局部结构
tSNE的局部结构更为紧凑。由于tSNE在拟合高维数据时使用高斯分布转换成概率,低维数据则使用t分布转换概率,这会使高维距离近的点在低维空间中更近,反之更远。
图4. tSNE通过两种分布模型的变换,使同样概率下,近者愈近,远者愈远,从而凸显局部结构
而UMAP设置了min_dist,在计算信息损失时,对低维距离小于min_dist的点视为同价,故而会隐藏一部分局部结构信息。
图5. UMAP将小于min_dist的低维距离视为等价
(三)耗时
tSNE的时间复杂度为O(n2),UMAP的时间复杂度为O(n1.14)。对数十万个流式细胞仪数据和单细胞数据进行降维时,UMAP较tSNE会有数倍甚至数十倍的速度提升。
图6 样本量越大,UMAP的速度优势越明显
(四)结果稳定性
tSNE使用随机分布初始化低维数据,而UMAP使用图拉普拉斯变换分配初始的低维坐标(根据高维数据特征进行低维数据的初始化),故UMAP的结果具有更高的稳定性。
图7. 100万个流式细胞(17个测量值)的降维结果,红色点为其中10%数据降维的结果,蓝色为完整数据降维的结果。UMAP的重合度明显更高,可见,UMAP对相似数据的降维结果更加稳定
三、重要参数及说明
(一)tSNE——perplexity
Perplexity(Perp)是tSNE调整高斯分布模型的重要参数。从可视化的角度讲,Perp会影响点的松散程度。Perp越大,集群内部越紧密;反之,集群越松散。从结构特征的角度讲,增大Perp将会增加高维远距离点的影响,使局部结构模糊;减小Perp则增加近距离点的影响,体现局部。但凡事有个度,Perp过大过小都会导致重要信息损失,或产生不必要的计算。在降维单细胞数据时,Perp建议设置为5-50,若要展示全局结构(效果未必佳),可适当增大Perp,但最大不超过(细胞数-1)/3。
图8. 3000个点的数据设置不同Perp进行tSNE降维的效果。全局结构的实际情况是两个集群较近,并远离另一个。
(二)UMAP——n_neighbors、min_dist
如图9所示,n_neighbors(即算法中的k)和min_dist会极大地影响UMAP可视化结果。n_neighbors与Perp相似,越大集群越紧密,且适当增加n_neighbors能更好地体现数据的全局结构。不同的是其含义,Perp约束全局与局部的软边界,而n_neighbors直接限定了各点受影响的邻近点数量。在实际应用中,n_neighbors最好大于较小集群内的点个数,防止有效的距离计算闭锁在集群内部,能更真实地反应全局结构。min_dist则可根据需求进行调整,较小值能更真实地反应高维结构,但也会带来一定的信息冗余,而上调min_dist能更直观地展示全局结构,同时有一定可能会反应错误的集群关系(如图10)。
图9. 同一个数据集在不同n_neighbors和min_dist参数下的结果变化
图10. 设置较大的min_dist,T细胞(紫色)被错误地与角质细胞(红色)聚成一类
四、高分文章tSNE和UMAP图展示
总之,由于算法特点,tSNE和UMAP各有所长。在论文绘图中,应根据表达的需要,选择合适的方法、调整参数。以下为近两年《Nature》、《Science》和《Cell》使用tSNE和UMAP作图的效果展示,供各位参考。
tSNE(Ren et al., Cell, 2021)
tSNE(Kuchina et al., Science,2021)
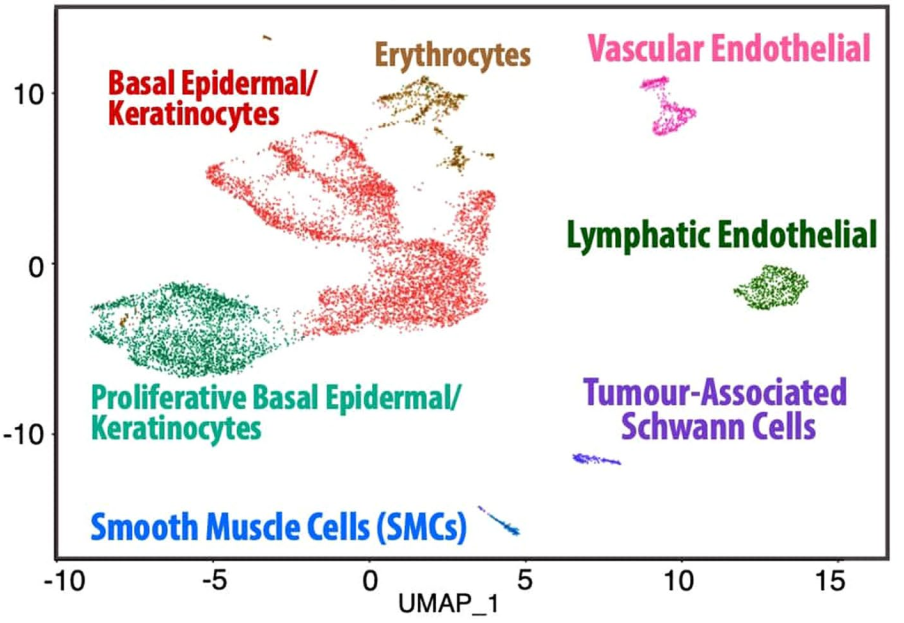
UMAP(Pascual et al.,Nature,2021)
UMAP(Wendt et al., Science,2020)
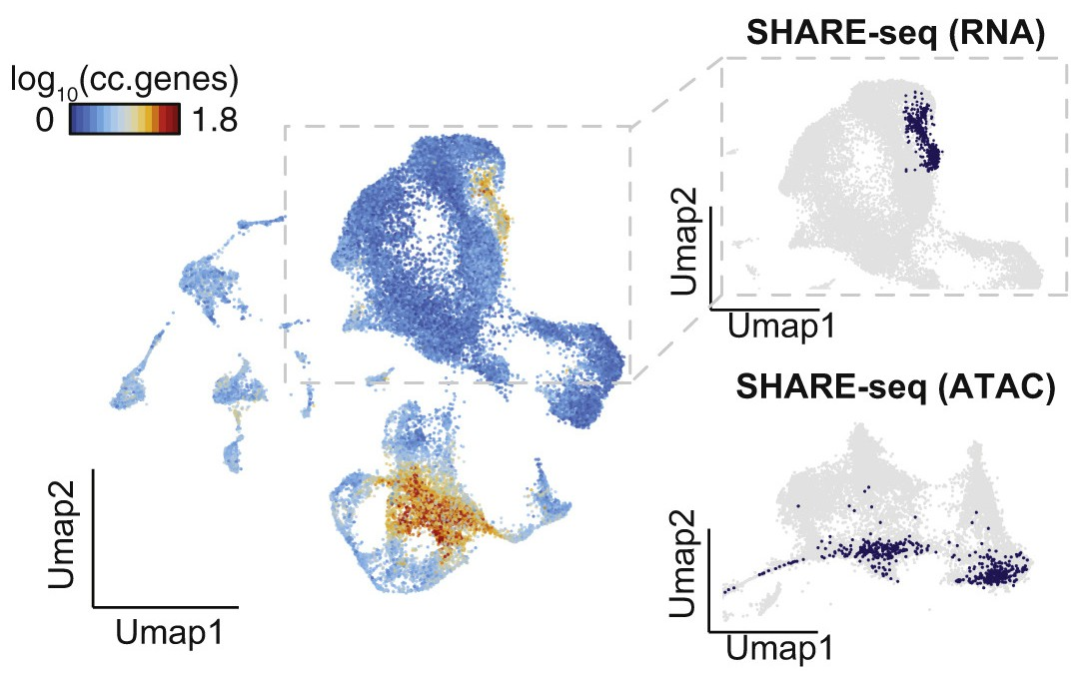
UMAP(Ma et al., Cell, 2020)
参考文献:
1. Der Maaten L V, Hinton G E. Visualizing data using t-SNE[J]. Journal of Machine Learning Research, 2008: 2579-2605.
2. Mcinnes L, Healy J. UMAP: Uniform Manifold Approximation and Projection for Dimension Reduction[J]. The Journal of Open Source Software, 2018, 3(29):861.
3. ANNA KUCHINA, XLEANDRA M. BRETTNER, LUANA PALEOLOGU, et al. Microbial single-cell RNA sequencing by split-pool barcoding[J]. Science, 2020, 371(6531).
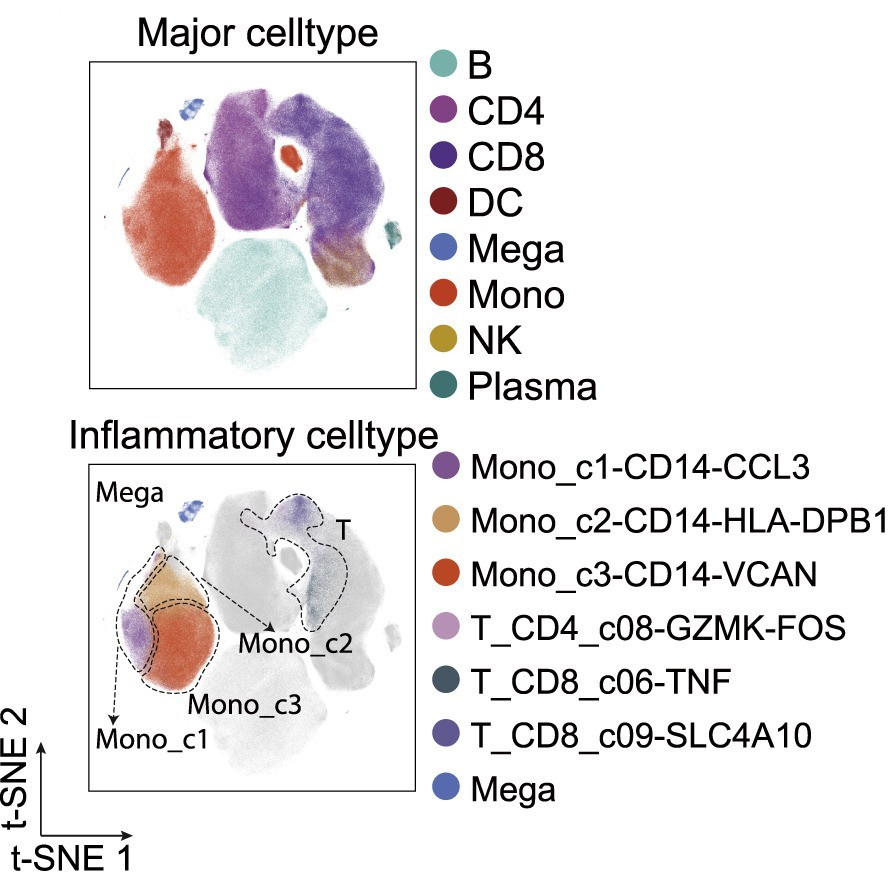
4. Ren X, Wen W, Fan X, et al. COVID-19 immune features revealed by a large-scale single cell transcriptome atlas[J]. Cell, 2021, 184(7).
5. Pascual, G, Domínguez, D, Elosúa-Bayes, et al. Dietary palmitic acid promotes a prometastatic memory via Schwann cells. Nature 599, 485–490 (2021).
6. Wendt G, Zhao L, Chen R, et al. A single-cell RNA-seq atlas of Schistosoma mansoni identifies a key regulator of blood feeding[J]. Science, 369.
7. Ma S , Zhang B , Lafave L M, et al. Chromatin Potential Identified by Shared Single-Cell Profiling of RNA and Chromatin[J]. Cell, 2020, 183(4):1103-1116.